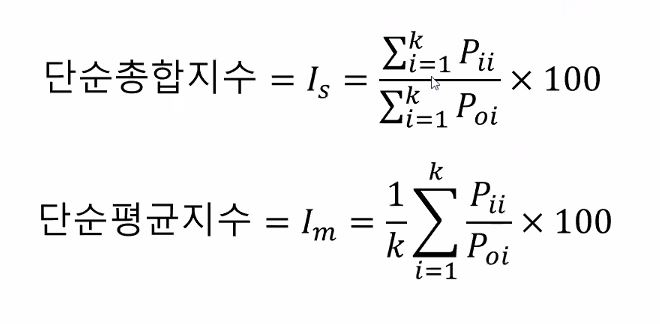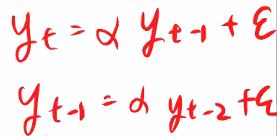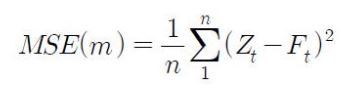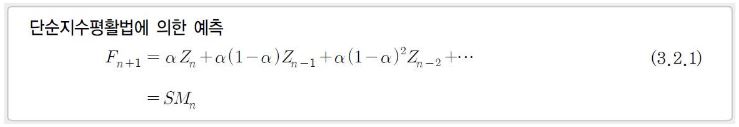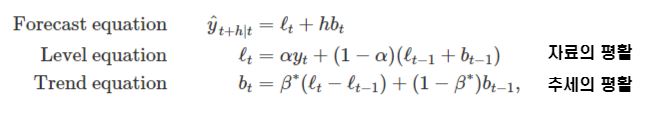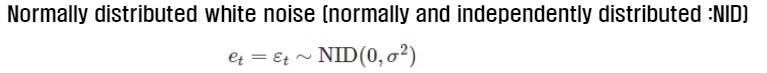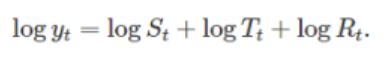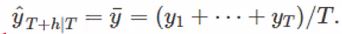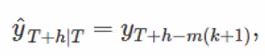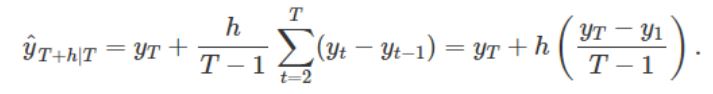Time-Series Analysis(1)

Intro

학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.

본 수업에서는 R 언어를 통해 1변량 시계열 데이터를 분석하고 ARIMA 등의 정상시계열 모형을 이용하여 예측하기까지의 실습 및 이론 수업으로 진행됩니다.

실습 환경 구축으로는 R 스튜디오 설치 정도가 있겠습니다.

실습 과제 1 보러가기

시계열(time series)

하나 또는 여러 사건(사상)에 대해 시간의 흐름에 따라 일정한 간격으로 이들을 관찰하여 기록한 자료를 말합니다.

어떤 경제 현상이나 자연 현상에 관한 시간적 변화를 나타내는 역사적 계열(historical series)

어느 한 시점 t에서 관측된 시계열 자료는 그 이전까지의 자료들에 주로 의존합니다.

그러나 그 이전까지의 여러 요인들의 (crisis 등)변화에도 영향이 존재하기 때문에 시계열의 법칙성을 발견해서 미래를 예측(classification 또는 regression)하는 것은 매우 복잡합니다.

수업에서는 시계열 데이터만의 규칙을 발견하고 이를 머신러닝 모델 또는 통계모형으로 이를 해결하는 과정을 다룹니다.

그러기 위해서는 패턴을 분석하는 것이 가장 먼저 할 일입니다.

그렇다면 시간의 흐름에 따라 불규칙적으로 변동되는 자료들도 분석이 가능할까요?

시계열 데이터에서는 변동 요인을 보통 4가지로 가정합니다.

변동요인

자료들의 특성을 단순화하는 것 입니다.

1. 추세변동(trend variation) 데이터를 보았을때 그 행보가 우상향으로 상승하는가, 하락하는가, 곡선추세인가 또는 횡보하는가 하는 변동

2. 계절변동(seasonal variation) 1년 안으로 반복적으로 나타나는 패턴들, 1년 동안의 월 또는 분기 등이 여기에 해당됩니다. 다음에 나오는 순환변동하고 구분할 수 있어야합니다.

3. 순환변동(cyclival variation) 계절변동과 비교했을때 보다 장기간의 term으로 반복되는 데이터를 말합니다. 계절변동으로는 설명되지 않는 장기적인 주기변동으로 이해하시면됩니다. 보통 추세변동이랑 같이 분석되곤 합니다. 그래서 회복기, 번역기, 후퇴기, 침체기 네 단계로 구성됩니다.

4. 불규칙변동(irregular variation) 위 세가지 변동으로 설명하지 못하는 경우에 해당합니다. 사전적으로 예상할수 없는 특수한 사건에 의해 야기되는 변동이나 명확히 설명될 수 없는 요인에 의해 발생되는 우연변동입니다.

우리는 주어진 시계열데이터를 위 네가지 성분으로 나눠 설명할 수 있습니다.

여기에 통계모형(?)을 적용시키게 되는 것 입니다.

• 승법모형(multiplicative model) Zt = TtStCt*It
• 가법모형(additive model) Zt = Tt+St+Ct+It

사실 우리가 머신러닝이나 통계모형 모델들 만으로는 완벽한 예측이 불가하죠, 이를 해소하는 것이 바로 오차입니다. 바로 장차값을 이용해 해결하는데 그것처럼 추세, 계절, 순환으로 설명할 수 없는 것에 대해 불규칙변동을 이용함으로써 해소합니다.

활용방법

지수(index number) 시계열 자료들의 변화동향을 비교하기 위해 특정한 시점을 기준으로 하여 백분비를 나타낸 값입니다.

지수 종류

1. 개별지수(individual index): 변수 하나의 계열을 비교하는 지수
2. 종합지수(composite index) : 여러 계열의 변화를 종합적으로 관찰하는 지수 ex) 단순지수

둘다 값은 하나인데, 여러가지의 값들을 포함시켜 결과값을 표현해낸게 종합지수라고 보면 됩니다.

단순지수 단순총합지수(simple aggregative index) : 기준시점에서의 단순평균지수(simple : dd

개별지수 예제 2005년 서울 지역의 쌀의 도매가가 가마당 48000원, 2010년은 72000원일때 2005년 기준 2010년의 지수는? 100*72000/48000=150% 참고로 2005년의 지수는 100%입니다.

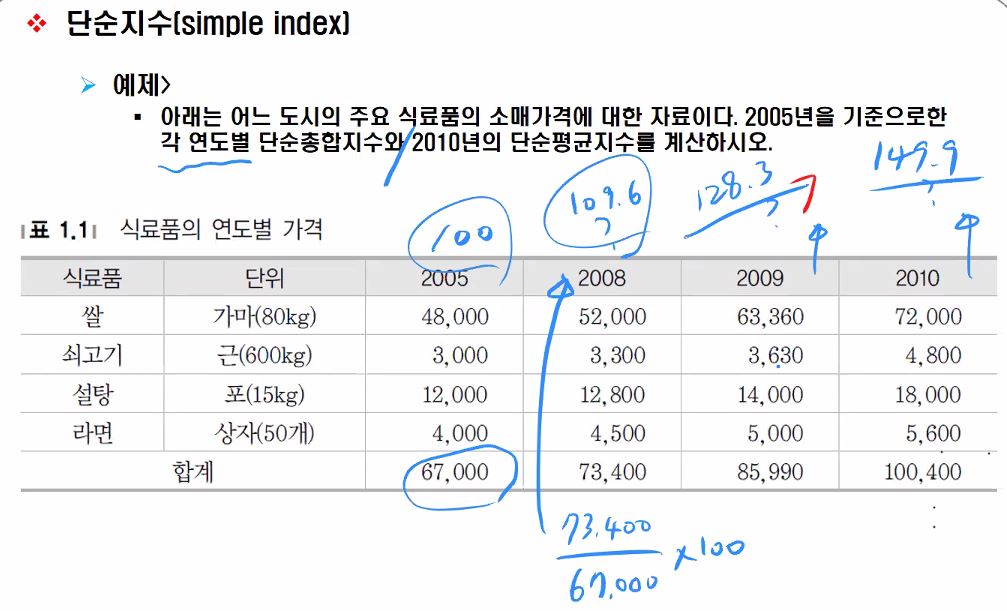
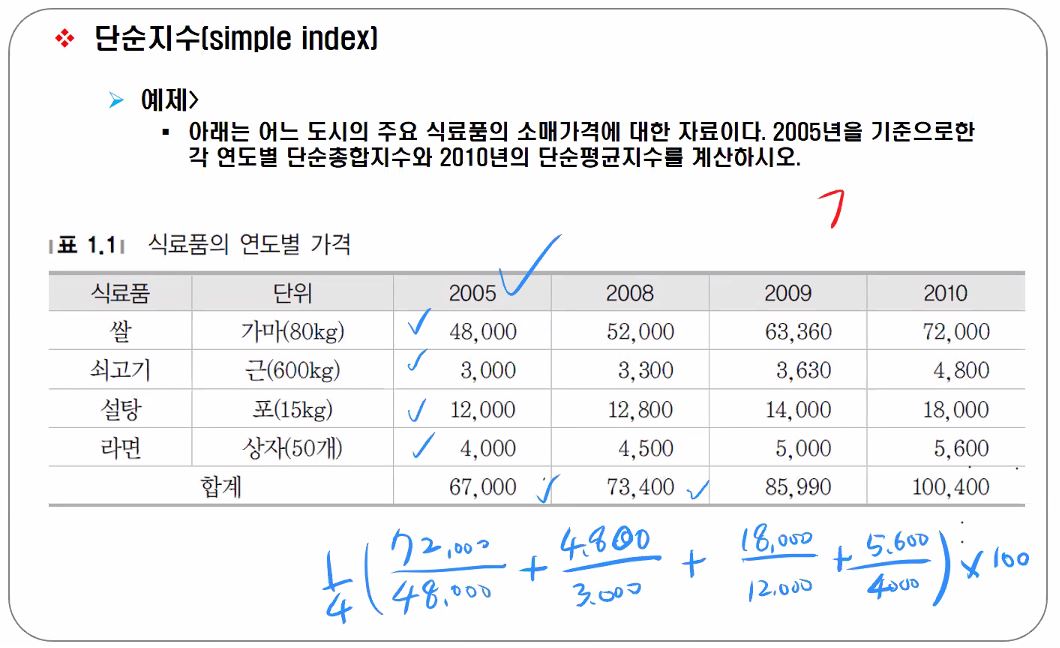
종합지수의 예인 단순지수 예제 아래는 어느 도시의 주요 식료품 소매가격에 대한 자료이다. 2005년을 기준으로한 각 연도별 단순총합지수와 2010년의 단순평균지수를 계산하시오.

시계열자료의 예측방법

(24페이지 뛰어넘음)

양적예측방법 구분 과거에는 데이터를 가장 잘나타내는 모형을 찾는 컨셉이었으나, 현재는 확률 통계를 기반으로 예측하도록 변해가는 추세입니다.

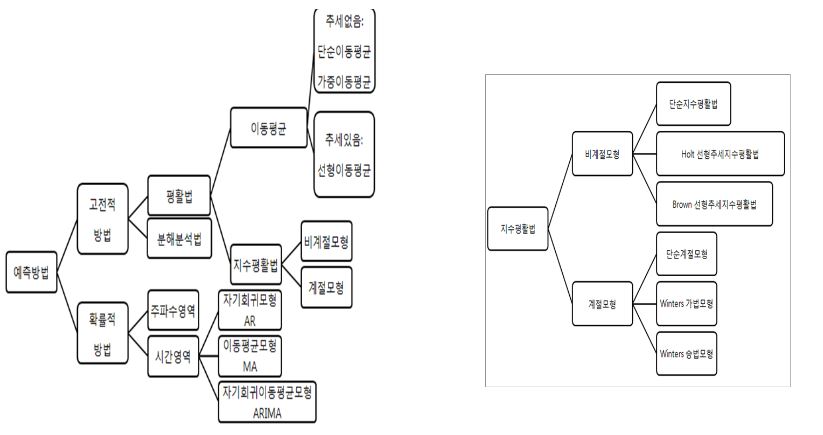
• 전통적 시계열분석방법 : 평활법(smotthing methods), 분해법(decomposition methods) 등
• 확률적 시계열분석방법 ML의 딥러닝, ML의 RNN, 시간영역분석(time domain analysis), ARIMA(autoregressive Integrated moving average), 주파수 영역분석인 퓨리에 분석(fourier analysis) 등

ARIMA에 0.4의 가중치를 두고 ML 모델에 0.6의 가중치를 둬서 섞어 쓰기도 합니다.

질적예측방법

전문가의 견해를 기반으로 예측합니다.

예측의 평가

보통 ML 모델 구축시 데이터를 train:test를 6:4 내지는 7:3 정도로 나누죠

시계열에서도 비슷합니다.

예측 평가방법 관측가능기간동안에는 모형의 추정 및 사전평가(validation)를 진행하며, 예측기간에는 사후평가입니다. 모형의 추정및 사전평가를 나눠할 수도 있고 함께 진행할 수도 있습니다.

보통 ML에서는 일반 data에서 sampling을 하여 train데이터와 test를 구분하는데, time series는 어떨까요? time series는 랜덤으로 sample을 뽑으면 안됩니다. 시간 순서가 중요하기 때문이죠. 대신 기간을 나눕니다.

순서가 꼬이면 미래의 데이터를 가지고 학습하는 셈이 되어버릴 수 있어서 유의해야합니다.

예측의 평가기준 평균제곱오차(Mean Squared Error, MSE) 평균제곱근 오차(,RMSE)(가장많이 사용) 평균절대오차(MeanAbsoluteError,MAE) 평균절대백분비오차(MAPercentageError) 타일의불일치개수

시계열분석의 가장 큰목적은 결국 미래에 대한 예측

고전적인 시계열 모형의 경우는 주어진 데이터를 얼마만큼 잘 설명할 수 있는가일 수 있지만 그래도 궁극적으로는 예측이 목적

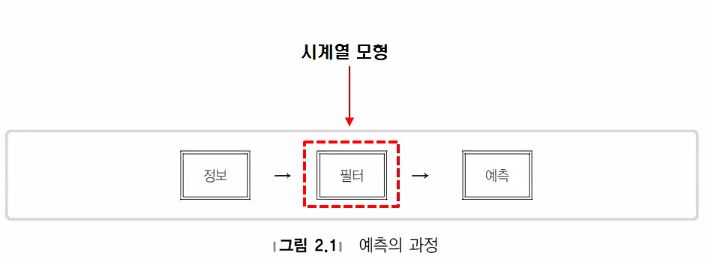
시계열자료의 예측방법 과거의 패턴은 미래에서도 지속된다는 가정 관측된 과거자료에 포함된 정보를 이용하여 예측에 필요한 경험적 법칙을 추정하여 예측 과거에 대한 정보가 알고리즘 내 존재

설명모형은 종속변수와 독립변수간에 인과관계를 설명하는 것 이를테면 주어진데이터를 가장 잘 설명하는 직선을 찾는것이 선형회귀분석이죠.

시계열모형은 생성과정이라는 표현을 쓰는데, t번째 Y값은 t-1번째 Y로부터 영향을 받아 생성된다 하는 정도로 해석하면 되겠습니다.

둘을 간단히 구분할 수 있습니다.

양적예측방법에는 전통적 시계열분석방법으로 평활법과 분해법을 배우게 되며, 확률적 시계열분석방법으로 시간영역분석인 ARIMA만 배웁니다. 퓨리에라고 주파수 영역분석방법도 존재하지만요.

예제를 봅니다. 예측력의 사후평가를 위한 MSE, RMSE, MAE, MAPE 그리고 타일의 U통계량을 계산합니다. (U는 자주사용되지는 않아요 그래서 다루지 않습니다)

실제값 - 예측값인 에러텀을 가지고 개선해내는것이죠. 물론 에러텀의 값은 작을 수록 좋은 것이구요.

이 측정값들을 test dataset으로만 볼것이 아닙니다. train data에 대해서도 봐야해요. 관측가능기간이 train단계, 예측기간이 test단계라고 보심 될 것같아요. 정확도를 예측하는 분류모델 (ex)accuracy)도 train, test 둘다에 대한 에러텀을 계산함으로서 나오는거에요.

모형의 일반화가 어려운 모델은 좋은 모델이라고 하기 어렵습니다.

사실 고전적방법은 잘 안쓸건데, 모델 비교 평가를 할때나 쓰겠네요

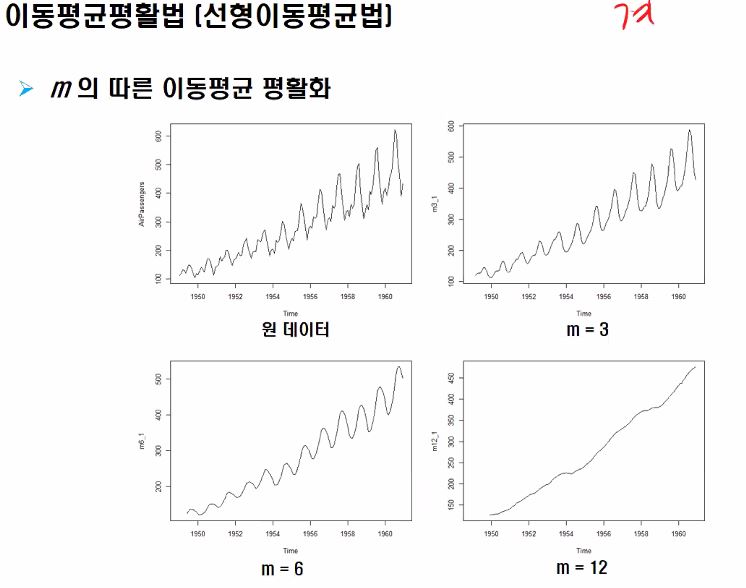
단순 이동평균법과 선형이동평균법을 이해해봅시다 단순이동평균법입니다. 계절성 불규칙성을 제거하여 전반적인 추세 파악 가능 가장 최근 m- 기간 동안의 자료들의 단순평균을 다음 기간의 예측값으로 추정하는 방법으로 m은 분석자에 의해 사전적으로 결정되며, m이 크면 장기 패턴, 작으면 단기 패턴을 진단합니다.

우리는 지금 이동평균평활법의 단순이동평균법을 적용해 예측하는 과정을 보고있습니다. 이동평균 기간 m이라는 파라미터는 관측기간 내에서의 MSE를 최소로 하는 값으로 결정하는 것이 좋습니다. MSE를 적용해볼거라한다면, 아래와 같은 식이 되겠습니다.

예제를 풀어봅니다.

forecast에 단순이동 평균이 없어서 직접 엑셀로 해보았습 겁니다. m=4~7일떄 각각, 차트까지 그리기

차트는 한번에 비교할 수 있도록 MSE를 구할때는 이동값들 기준이니까 데이터 개수를 맞춰서 가장 적은 m==7일때의 개수에 맞춰서 관측된 시계열이 선형 추세성을 갖는 경우에 선형이동평균을 사용(이중이동평균)하면 더 좋다 m은 이동평균 계수 값 이중 이동평균은 한번 더 이동평균을 구하는 것을 말합니다. 현재 시점이 n인 경우에 n+l 시점의 값을 예측하는데, 보통 l=1인 경우가 많습니다. 딱히 식을 외울 필요는 없습니다. 다만 M 값이 무엇인지는 알아야합니다. 14번 슬라이드의 예제는 t=6일때의 값을 예측하고자한 것입니다. 한번 연습을 해보세요..

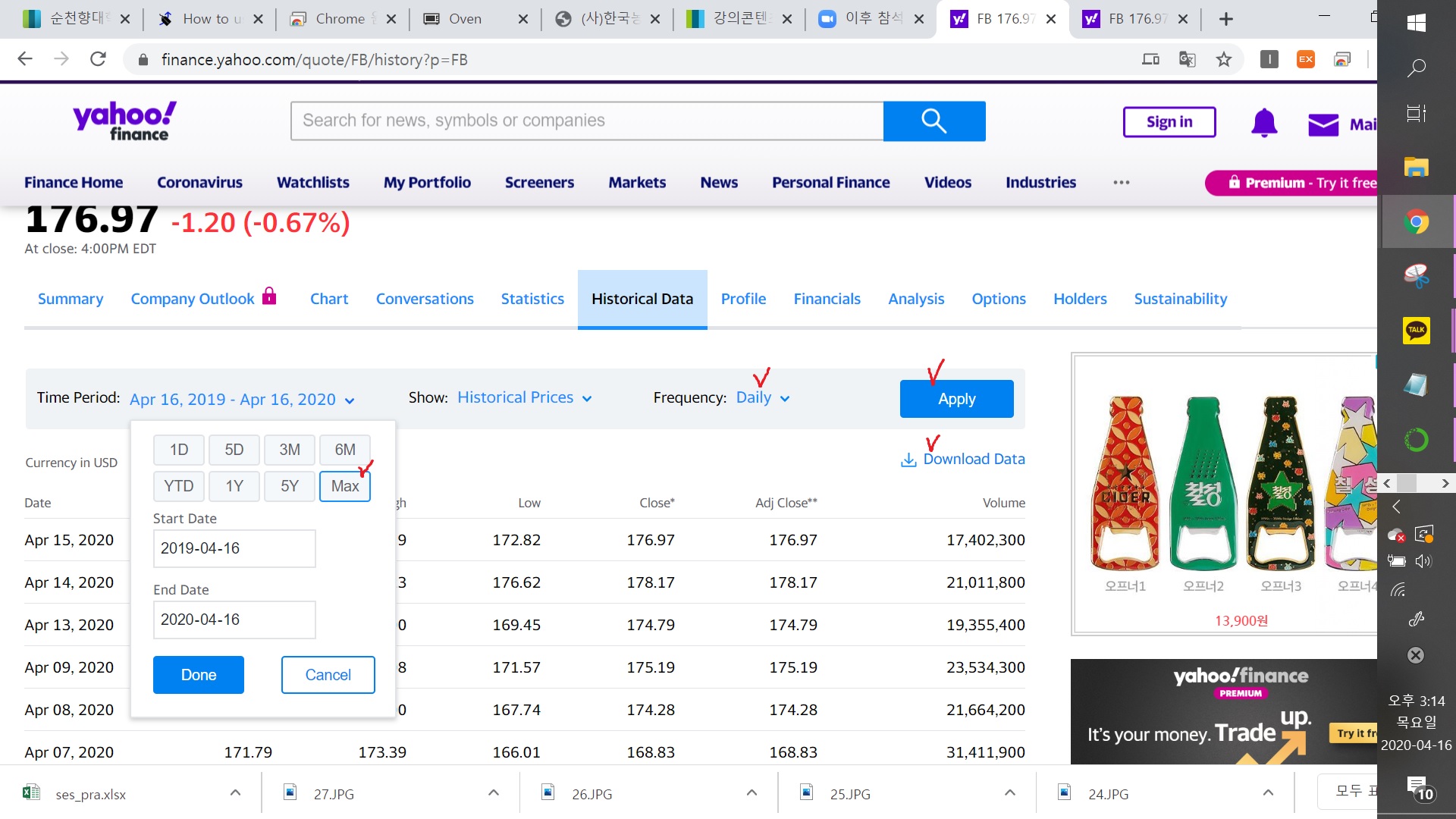
페이스북주식가격을 바탕으로 평활화하기 단순이동평균법은 계수 m개를 가지고 평균을 계산하죠 동등하게! 가중이동평균법은 최근 데이터에 0.5를 곱하고 과거로 갈수록 0.3을 곱하고 0.2를 곱하고… 이렇게 하는겁니다. 원데이터에 가중치를 곱하고 다 더합니다. 가중치는 한번 정했으면 고정입니다.

엑셀로 분석 합니다. fb 데이터가지고 실습할거에용.. https://finance.yahoo.com/quote/FB/history?period1=1337299200&period2=1586995200&interval=1d&filter=history&frequency=1d

단순이동평균법은 계절성, 불규칙성을 제거하여 전반적인 추세 파악이 가능하다고 배웠습니다.

원데이터의 경우는 어떤 패턴이 있습니다. 계절성은 어느정도 드러나지만 m=12까지 갔을때를 보면 어떤 추세만이 드러난다는 것을 알 수 있습니다.

이동평균을 가지고 예측하는 것을 많이 하지는 않습니다. 예측방법보다는 주어진 데이터를 얼마나 잘 설명할 수 있는지에 초점을 두고 학습하면 좋을 것 같습니다.

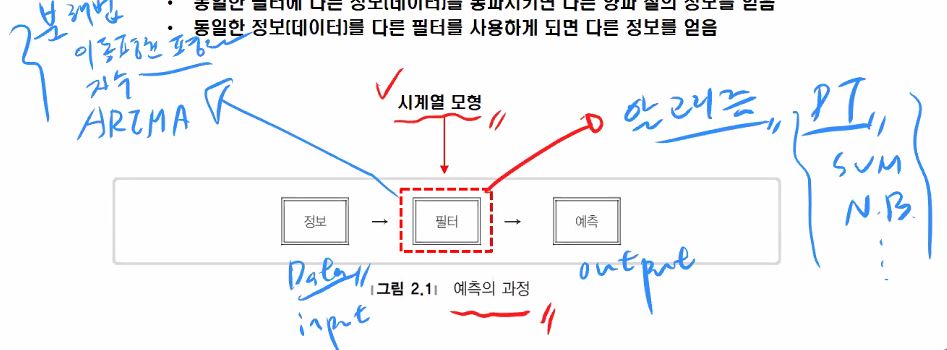
시계열 분석의 워크플로우는 input > filter > output이었죠. 이동평균법도 마찬가지로 filter에 속합니다.

단순지수평활법

오늘은 단순지수 평활법을 배웁니다.

R의 forecast 패키지의 ses함수를 이용해서 실습도 해보겠습니다.

단순지수 평활법은 시계열 관측값들에 대한 전체적 가중평균인 평활값으로 미래의 관측값을 예측합니다. 단순이동평균법과는 달리 최근 자료에 더 많은 가중값을 부여하는 방식으로 0~1사이의 값을 갖는 알파라는 평활상수에 의해 지수적으로 과거로 갈수록 그 값이 미미해지게됩니다.

식을 전개해 적용하다보면 아실거에요!

F는 예측값 Z는 관측값이라고 보시면 됩니다.

이제 바로 위 데이터를 가지고 R로 실습해봅시다.

• 실습 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/simple_exponential_smoothing_exmaple.ipynb
  

단순지수평활법에 해당하는 ses()를 호출할 때 인수들로는 가장 중요한 alpha값을 0.2를 포함해 ts 객체와 초기값 그냥 그대로 가져오는 simple설정을 함께 넘겨줍니다.

각 오차함수값들을 확인해보세요!

단순지수평활법은 아주 잔잔하고 추세나 계절성이 없는 데이터들에 적용하면 좋은 분석법입니다.

이번엔 optimal로 계산을 한번 해봅시다 파라미터로 h=3 으로 주게되면 미래값을 3개정도 예측해서 보여달라는 뜻이 됩니다.

초기값을 optimal로 하게되면 초기값하고 알파값도 optimal(최적)한 값으로 찾아서 알아서 해줍니다.

(24페이지까지 실습해볼것 fb 데이터 가지고 이동평균, 선형이동평균, 가중이동평균 엑셀로 분석하고 각 평활법 별 차트그려주시 월요일전까지..)

예측하는 것 뿐아니라 데이터를 분석할 줄 알아야 합니다. (엑셀과제캡처첨부) m=120인 경우가 장기패턴, m = 60인 경우가 중기패턴, m = 5인경우가 단기패턴으로 나눠보기도 합니다.

전반적으로 그래프 자체도 원인대비 결과 값 자체가 5>20>60>120 이렇게 나오는데, 우상향추세까지만 끊어보면 상승상세를 보이며, 이후 떨어지기 시작하는 시점 즉, 골드크로스 때 부터는 반대로 5<20<60<120 의 하락상세를 보이게되는 것을 확인할 수 있습니다.

예측을하려면 한칸씩 미뤄서 보지만, 예측이 아닌 데이터를 설명하기위해서는 현재값을 포함해서 봐야 바람직합니다. 왜냐하면 미래값을 가져다 쓴 셈이 되기때문입니다.

저처럼 예측이 아닌 데이터를 설명하는 목적으로 사용하게되는 경우의 오차는 무슨의미가 되는건지 잘모르겠습니다! 가 궁금하시다면, 예측을 평가할 때에는 예측력 측도로 MSE, RMSE 등을 사용하지만 시장 장세, 데이터를 설명하기 위한 용도로 이동평균을 사용한 경우에는 그에 맞는 별도의 측도를 이용합니다. 그리고 그럴 때 사용되는 RMSE나 MSE는 예측 오차라고 부를 수 없습니다.

적합데이터(즉, 학습)를 위해 사용된 함수며 “잔차”라고부를 수도 있습니다. 잔차를 summation해서 보여준 “목적”함수에요! 즉 용어의 차이이며, 방법은 같습니다.

상승하는 구간, 하락하는 구간, 횡보 등의 패턴에 따라서 어떤 형태의 분석이나오는 지를 살펴보는 것도 좋을 것입니다!

단순지수평활을 적용해본 두 번째 실습을 진행했습니다. 알파값을 0.1, 0.5, 0.9로 두고 마지막으로는 최적값을 두고 실습을 진행해보았으며 그 결과를 분석해봅시다.

• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/simple_exponential_smoothing_exmaple2.ipynb
  

알파값이 0.1인 경우에는 존재하는 데이터에 대한 예측이 원본데이터를 전혀 따르지 않아 예측에 사용이 불가능한 수준이라고 볼 수 있습니다.

알파값이 커질수록 원본데이터와 점점 비슷해지며 잔차값이 줄어드는 것을 확인하실 수 있습니다. 0.9 알파값의 경우 마치 한칸 밀어놓은 것처럼 생겼는데, 이럴경우는 예측에 사용이 가능할까요? 아니요 마찬가지로 사용할 수 없습니다!

참고로 만약 알파가 1이라면 정말 말 그대로 한칸씩 당긴 것이 됩니다. 수식에 알파값을 대입해보면 알 수 있습니다.

각 fit 이후에는 names()로 각 변수를 찍어보게 되었는데요 변수마다의 의미를 살펴봅시다.

• model : 모델에 관한 정보
• method : simple인지 optimal인지
• mean : 각 관측치의 평균점
• level : 신뢰수준
• x : 원본값
• residuals : 적합된 모델과 원본데이터 간 잔차
• fitted : 적합된 값
• lower : 예측구간 하한값
• upper : 예측구간 상한값
  
  

+ 추가 지식 신뢰구간 : 해당 모수값이 존재할 것으로 예측되는 구간입니다.
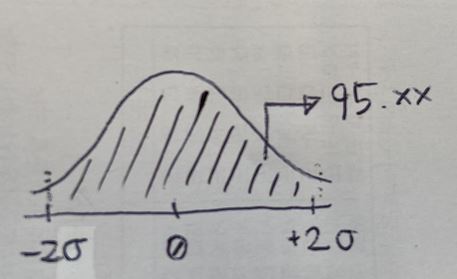
80이라하면 80%로 해당 구간에 존재할 확률이며, 95는 95%로 해당구간에 존재할 확률이라 더 넓은 범위를 갖는겁니다.

신뢰구간은 보통 잔차의 표준편차와 1-승수의 곱으로 계산이 됩니다. 적합이 잘 되면(잔차의 표준편차가 작으면) 신뢰구간의 폭은 작아질 겁니다.
예를들어 1.96 * 표준편차는 95% 신뢰수준인 경우 입니다.

신뢰구간이 뒤로갈수록 더 넓어지는 이유는 h 의 값의 곱으로 인해 나타나는 현상인데, 시간이 멀어질수로 비례해서 커집니다.
안커지는 것 같아도 미미하게 커집니다.. 약간이라도 커지는데 아마 표준편차가 넘 커서 h와 비례하게 넓어지긴 하는데 이게 루트형태로 곱이라 눈에 안띌 뿐입니다!

더불어 예측값의 정확도와 신뢰구간이 넓고 좁고는 별개의 이야기며, 신뢰구간 넓이의 문제는 적합이 잘되었는지 여부와만 직결되는 문제인걸로 이해하실 수 있겠습니다!
예측의 정확도는 RMSE등의 잔차 측도로 평가할 수 있겠습니다.

홀트의 선형지수평활법(Holt’s linear trend method)

아주 잔잔하고 추세나 계절성이 없는 데이터들에 활용하는 단순지수평활법과 달리 홀트의 선형지수평활법은 추세가 있는 데이터를 예측할 수 있도록 단순 지수 평활을 확장한 모형이며, 두개의 평활식(수준에 관한 것, 추세에 관한 것)으로 이루어집니다.
수준식은 관측값의 가중 평균(=자료의 평활)이며, 추세에 관한 식은 말 그대로 추정된 추세의 이동 평균(=추세의 평활)입니다.
예측 함수는 더이상 평평하지 않고, 추세를 가집니다.

다시 정리해봅시다.
홀트의 선형지수평활법은 자료의 평활과 추세의 평활로 구성됩니다.
자료의 평활만 보면 단순지수평활이랑 거의한데, 거기에 추세의 평활이 더해진 것 뿐 입니다!

2개의 최적 알파와 베타를 추정하게되는데, SSE(sum of squared error)로 추정합니다.

홀트의 선형지수 평활법도 실습을 한번 해봅시다.

(홀트의 선형지수~40번슬라이드까지 실습해보기 damped true로 설정하고 안하고 차이 비교해보기)

• 실습 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Holt’s_linear_trend_method.ipynb
  

+추가 지식 어떤 데이터엔 어떤 모형이 적합하다, 이 모형을 활용하는 것이 좋다 하는 기준이 뭔지 궁금했는데, 경험적으로 또 통계적으로 이런 모형을 썼을 때 잔차값이 작아서 특정 모형이 어떠한 변동을 띄는 데이터에 좋다라고 말할 수 있다고 합니다.

홀트계절지수평활법(Holt-Winters’ seasonal method)

월별, 분기별 자료들은 보통 계절변동을 포함(추세+계절+자료변동(=level))하는 경우가 많습니다.
참고로 자료변동은 불규칙에 포함됩니다.

이렇게 데이터에서 계절성이 보인다면 계절지수평활법을 적용하는 것이 좋습니다.
파라미터로 구분되는 두가지의 메소드가 있습니다.

• 승법적 계절지수평활법(곱하기 이용)
  
• 가법적 계절지수평활법(더하기 이용)
  

추세에 관련된 식 하나, 계절에 관련된 식 하나, 자료변동에 관한 식이 또 하나 나올건데 이 세 식들을 다 더해서 해결하면 가법적인 것이고, 곱해서 이용하게되면 승법적인것이 되는 것입니다.

forecast 패키지를 이용한 실습에서 사용하는 함수로는 hw라고 표기하며 그 안에 승법으로 할지, 가법으로할지 고르면 됩니다.

그렇다면 둘 중 어떤걸 어떤 때에 사용하면 될지 확인해봅시다.
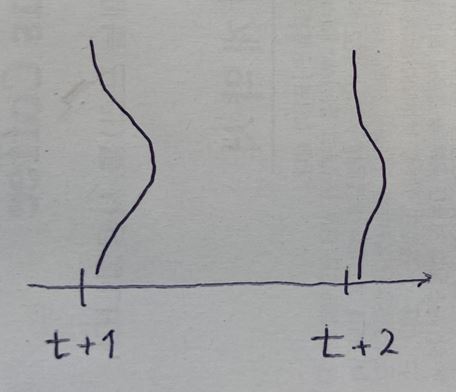
시계열의 계절적 진폭이 점차적으로 증가/감소하는 특성을 가지면 승법, 시간의 흐름에 따라 진폭이 일정한 특성을 가지는 경우엔 가법적을 사용하시면됩니다.

다시 한 번 설명하자면, 왔다갔다 진동하는것이 기본적으로 계절적 변동인데, 높낮이가 일정하면 가법적, 진폭이 점점 커지거나 감소되는 데이터의 형태는 승법적인 모형을 적용하시면 됩니다.

우리는 탐색적으로 데이터를 먼저 도식화해보고 어느 모형을 쓸지를 결정하면 됩니다.
하지만 확실하게 눈에 띄는 경우에는 바로 사용가능하겠지만, 잘 드러나지않고 헷갈린다면 둘다 써보면 됩니다.

• 실습1 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Holt-Winters’%20seasonal%20method.ipynb
  

• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Holt-Winters’%20seasonal%20method2.ipynb
  

(2020-04-28) 어떤 모형이 더 낫나를 판단할 때 그 판단에 대한 측도는 무엇일까요? 우리가 배운 측도는 RMSE와 MSE 밖에 없었어요! 참고로 어느 모형이 더 적합한지, 예측력이 높은지는 서로 다른 측도로 평가합니다.

신뢰구간은 정규분포에 기반합니다.

h값에 따라 시간이 흐르면 흐를수록 점점 더 예측력이 흐려지게 될 것입니다.

시뮬레이션 기능이 있어서 수천번 돌려보면 어떻게 나오는가를 확인해볼 수 있어요. 어쨌든 중요한 것은 뭐냐면 신뢰구간과 예측력은 상관없다는거죠. 그래서 평가 측도는 RMSE로 평가하면 되는데, RMSE는 잔차 제곱들의 평균에 루트 씌운거잖아요? 이 때 잔차는 실제값(y)-예측값(y햇)이구요. 그런데 사실.. 신뢰구간에는 y햇(예측값)만이 존재합니다. 실제값이 얼만지 알수가 없기 때문에 좋다 안좋다 말하기 어렵습니다. 통계적 측정모델로서 RMSE 값을 보고 어느 모형이 더 나을지 보는 것이 최선이죠. 다시 말해 잔차분석이 최선이라는 뜻입니다. 잔차에 어떤 패턴이 남아있으면 그 모형은 잘 적합되지 않았다고 말할 수 있는 셈입니다. 우리는 이 수업을 통해 잔차들에 대한 그래프를 여러 번 그려볼건데 그 그림에서 패턴이 남아있다면 적절한 모형을 쓰지 않았다는 것이 된다는 점을 알아야합니다.

홀트윈터스에서 세 공식들이 있었지만 이 커리큘럼 내에서는 그 식들을 다루지 않았어요.

상태 방정식을 확인하려면 fit_aust_add$model$states fit_aust_multi$model$states 등의 코드를 통해 확인하실 수 있습니다.

ETS(Error, Trend, Seasonal)

오늘은 잔차나 에러텀이 없는 여태까지 배운 모형들과 다르게 확률적 시계열 분석법을 배웁니다.

여기에는 ets 모형이 표기 안되어있지만 확률적방법에서 시간영역에 포함될수 있겠습니다.

우리가 알고 있는 선형회귀모형식에는 입실론이 들어가죠?

이전까지는 잔차를 사용하지 않고 파란부분까지만 계산했다면 전시점데이터랑 예측사이의 잔차에 대한 새로운 텀을 추가해주는 것입니다! 입실론(에러)텀이 추가됩니다.

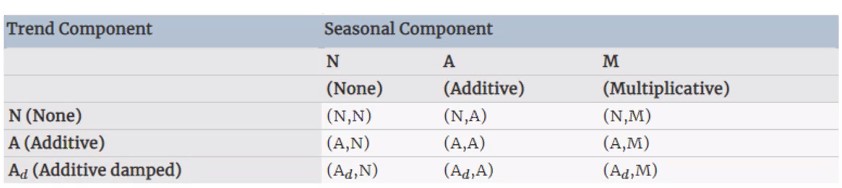
이전에 배운 모형들을 기반으로 조합하여 정리하면 아래처럼 아홉가지 메소드가 나오게 되는데요,

추세에는 multi는 없어요 원래 만들 수 있긴한데 댐프드만 있답니다.

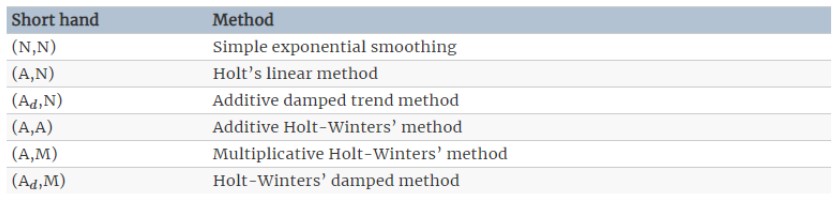
이 아홉개중에 대표적으로 많이 사용하는게 아래 표에 정리되어있습니다.

맨 마지막 모형을 빼고선 다 실습에서 다뤄봤지요!

오늘은 ETS(Error, Trend,Seoasonal) 모형을 배웁니다. ETS(A,N,N)은 배웠던 단순지수 평활법에 error 텀을 더해준 것입니다. Simple exponenetail smoothing with additive errors라고 말할 수 있어요 확률적인 통계기법이 모형에 들어간다고 말할 수 있어집니다. 그렇다고 해서 무조건적으로 좋은건 없답니다. 어느 모형이 이 데이터에 적합한가는 비교해서 보아야 합니다! RMSE를 비교해본다던지 하는 방법으로요..

• 실습1 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/ETS_example.ipynb
  

위 실습 내용을 확인하셨다면, ZZZ로 설정했을 경우 무슨 값을 기준으로 최적 모형을 자동으로 찾아주게 될까요? 정보손실 기준이라고하는 AIC, AICC, BIC를 기준으로 찾아주게 됩니다. 이 값들이 작을수록 해당 모형이 선택될 확률이 큽니다. 이 커리큘럼에서 이내용을 학습하지는 않지만 보통 이 세 값이 작으면 RMSE도 작은 경우도 많습니다.

우리가 ETS를 이해하기 위해서는 기존까지 저희가 배웠던 모형에서 에러텀을 추가하는 형식으로 식을 변형하여 이해할 필요가 있습니다.

위 식대로라면 이렇게도 되겠지요? 똑같은 식인데 표현을 바꿔본거라고 보시면 됩니다.

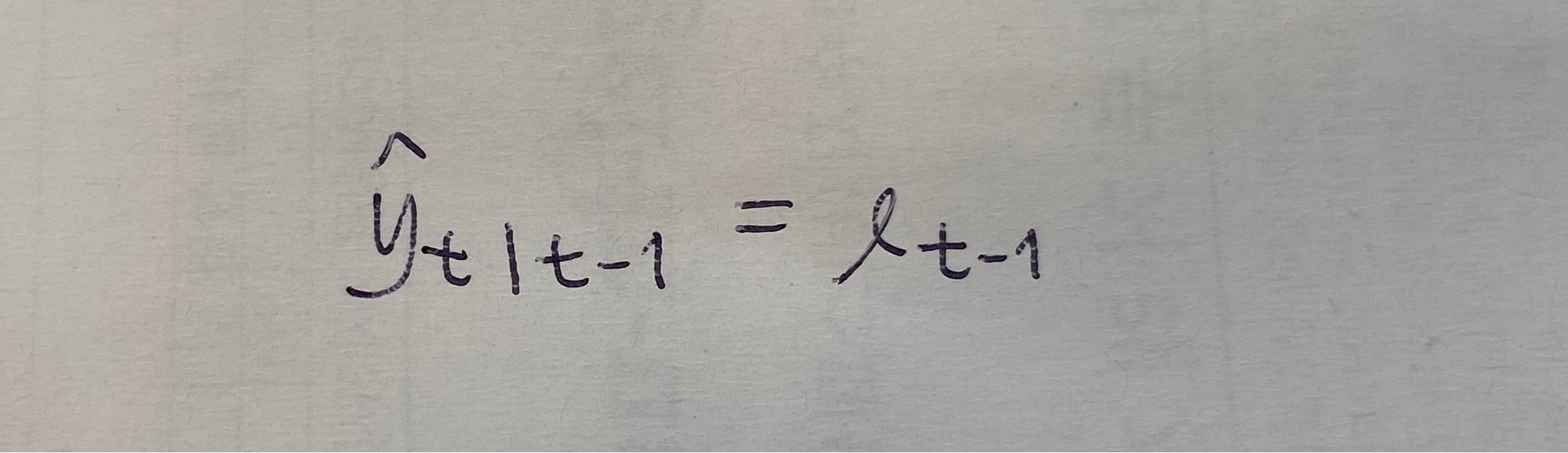
에러텀은 아래와 같이 정의됩니다.

NID 또는 IID라고도 부릅니다 ‘평균은 0이고 분산이 일정한 형태를 갖는다’고 이해하면 됩니다. 여기까지는 가법모형에 해당하는 형태이구요,

승법모형도 보겠습니다.

R의 forecast패키지에서 제공하는 ETS()의 model 매개변수의 첫째 자리는 에러텀을 승법(M)으로 할것이냐 가법(A)으로 할것이냐를 말하며, 나머지 두자리는 그전에 배운 것들로 나뉘어요!

아까damped만있구 multiplicative없다고 했었죠? 그래서 ets()의 가운데 인수는 M으로 둘 수 없습니다 .(이론상으로 만들 수 있긴한데, 모형이 잘 드러맞지 않아서 사용을 안한다고 합니다.).
또 첫번째 인수(error term)역시 N으로 둘 수 없습니다.

ets모형은 forecast()를 별도로 호출해야 예측을 합니다.
accuracy() 함수를 이용하여 예측 평가를 위한 함수입니다.
에러텀이 있고, 없고의 차이를 보이며, 그러기 위해 Training set과 test set을 따로 두어 성능 평가를 진행하는 두 번째 실습예제의 링크를 걸어드리겠습니다.

• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/ETS_vs_HW_example.ipynb
  

우리는 ses이용과 ets 이용을 하여 시뮬레이션까지 돌려보고 비교해볼 것입니다.

주식 시장에서도 몬테카를로 시뮤레이션이라는 통계적 기법을 활용해서 수만번 시뮬레이션을 해보고 예측에 사용합니다.

• 실습 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/ses_vs_ets.ipynb
  

여기까지 배우게 되면 ETS까지 추가적으로 배우긴 했지만 우리 커리에서 다루는 고전적 모형은 다 배운 것입니다. 이동평균을 제외하고 우리가 배웠던 분해분석쪽의 지수 평활법들과 ETS를 최종 비교해보는 실습을 해봅시다.

• 실습1 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/comparing_all_of_exponential_smoothing_method_wih_ets_1.ipynb
  
• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/comparing_all_of_exponential_smoothing_method_wih_ets_2.ipynb
  

이러한 파라메터를 갖는 시계열 모형의 경우에는 모형이 적합한가를 평가할 때에 파라미터들이 0에 가깝다면 RMSE값은 낮다하더라도 적합하지 않을 가능성도 있습니다.
그래서 히스토그램을 그렸을 때 정규분포형태로 나와야 잘 적합된 것이라고 확인해볼 수도 있습니다.

후에 추가적으로 학습할 예정입니다.

분해법

시계열 데이터 분석의 예측 방법의 고전적 방법에는 앞서 배웠던 평활법과 분해분석법이 있습니다.
이번 시간에는 분해분석법에 대해 학습합니다.

평활법에 의한 예측방법의 경우 특정 패턴이 시계열에 내재되어 있을 때, 이 패턴은 원계열을 평활하여 불규칙변동을 제거함으로써 추정이 가능하다는 것이 전제되어 있습니다.

분해법에 의한 예측방법의 경우엔 시계열의 패턴을 부분패턴으로 분해합니다.
이를테면 패턴(혹은 변동요인)을 개별 성분으로 분해하여 시계열의 특성을 분석합니다.

여기서 개별 성분은 앞서 배웠던 추세변동, 순환변동, 계절변동, 불규칙변동으로 구성됩니다.

분해된 각 성분들을 개별적으로 예측한 후에 이들을 다시 결합시켜 예측을 실행합니다.

참고로 순환변동은 장시간에 거쳐 확인할 수 있는 변동으로 추세변동과 합쳐서 함께 성분으로 두고 분해하곤 합니다.

계절성분은 S로 표기하며, T는 추세순환성분, R은 불규칙성분입니다.

분해법의 목적은 예측에도 사용될 수는 있지만 계절조정입니다.

이 세 텀을 모두 더하여 타겟 변수 y를 계산한다면 가법 모형(additive decomposition)을 적용하는 것이며, 모두 곱하여 타겟 변수를 계산한다면 승법 모형(multiplicative decomposition)을 적용한 것입니다.

Cf) 승법 모형에 로그변환을 하게 되면 로그함수 특성상 가법모형으로 전환이 가능합니다.

시계열 데이터의 변동 성분들을 추세순환성분과 계절성분 불규칙 성분으로 나누기로 했는데, 이 중 이동평균방법을 활용해 추세순환성분을 추정합니다.

평활법 배울 때 초기에 이동평균평활법을 배웠었죠? 불규칙 성분들을 제거하고 추세-순환성분을 추정하기 위해 사용했었습니다.

시계열 분해를 위한 이동평균 역시 Order selection 기반인 것은 똑같습니다.

대칭이동평균은 m이 홀수인 경우에 사용하며 중심화이동평균은 m이 짝수인 경우에 사용합니다.

앞서 배웠던 이동평균과 어떤 차이점이 있는지 찾아봅시다.

3MA가 홀수인 경우(대칭이동평균)고 4MA와 2*4MA가 짝수인 경우(중심화이동평균)죠.

참고로 2*4MA는 이중이동평균입니다.

차이점은 바로 예측값을 작성하는 행의 위치차이입니다.

3MA일경우 1,2,3의 평균을 t=4 행에 썼었는데 여기에서는 1,2,3의 평균을 t=2 행에 쓰네요.

근데 짝수의 경우에는 저렇게 쩜오행에 써야하는 상황이 오는데 그럴 경우는 t가 몇 일때의 적합값이라고 말해야 할까요?
그래서 이중이동을 해주는 겁니다.

이동평균법을 이용한 추세-순환성분 추정에 대한 실습을 진행해보았습니다.

• 실습1 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/decomposition_ex1_MovingAverage_for_the_trend-cycle_component1.ipynb
  
• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/decomposition_ex1_MovingAverage_for_the_trend-cycle_component2.ipynb
  
• 실습3 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/ma_for_decomposition.ipynb
  

정리하면, 오늘 배운 이동평균이 여러 변동중에 추세-순환변동을 추정하기위해서 평활화하는 방법이고, 이후에 배울 다른 메소드들로도 계절성분을 추정해서 그들을 곱하거나 더하는(승

가법 모형) 것입니다.

참고로 불규칙을 추정할 수 있는 메소드는 없습니다.
그러면 S구하고 T구하면 R은 어케 구할까요?

실제값이 있으니까 거기서 빼면 R도 구할 수 있겠지요.

불규칙은 추정이 사실상 불가능하고 그럼 계절성분과 추세순환성분을 어떻게 추정하느냐 문제인데, 어떻게 추정하냐에 따라서 조금씩 달라집니다. 그리고 이 수업에서는 추세순환성분을 추정할 때 이동평균법을 쓰는 것뿐입니다.
계절성분뽑아낼 때 고전적인 방식으로 뽑아냈더니 연도별로 똑같이 나와버리는 문제점이 있어서 더 나은 모형을 적용시켜보며 발전해온 것입니다.

1/2씩 더 곱해진다는 것을 알 수 있습니다.(13)
M=홀수냐 짝수냐에 따라서 다른 방법을 적용해주어야하는데 월별/분기별이 아무래도 많습니다.

이동평균을 이용하는 고전적 분해법 중 하나인 Classical decomposition을 학습합니다.
승법과 가법으로 나뉩니다.

Seasonal 성분을 보면 2000년도에 Q1이 50, Q2가 60, Q3가 40, Q4가 50이었다면 2001년도의 Q1~Q4는 무엇일까요? 똑같습니다.
2002년도에도 똑같습니다.
Classical decomposition이라는 분해법이 그렇게 만들어줘요!
추세 조정된 시계열을 바탕으로 주기별로 평균을 계산한 후 주기별 평균의 합이 0이 되도록 조정합니다. 그러면 저렇게 같게 나오게 됩니다.

다시 한 번 정리해보겠습니다.
MA로 적합 후 trend를 확인해보면 Ma의 특성상 앞뒤 정보를 손실한다는 문제점을 가지고 있습니다. 어쨌든 그렇게 구한 T가 있을거에요.
그 다음 계절성분을 추정하는데, 전통적인 방법의 경우 추세조정된 계열(y-T)을 바탕으로 주기별로 평균을 계산한 후 주기별로 평균의 합이 0이되도록 조정하며 S를 구합니다.
그러기 위해서는 주기별로 평균 계산한 것에서 주기별 평균의 평균 계산값을 빼주어(분산) 해당주기의 대표값으로 사용하게 되는데 그 주기별 대표값들을 다 더해보면 0이된다는 것을 알 수 있습니다.
그 이후에는 y-T-S를 통해 불규칙성분인 R을 뽑아낼 수 있겠지요.
이렇게 구한 T와 S와 R이 나오면 이들을 더했을 때 원본데이터가 되는 겁니다.
이 문제는 잠시 말했던 것처럼 양 옆이 잘렸다는 것이죠. 그럼 랜덤을 뽑아내거나 할 때에도 문제가 있다는 것입니다.

승법모형은 다 똑같은데 빼는게 아니라 나누는 것만 차이가 있어요.
그래서 대표값들을 다 합쳤을 때 12가 됩니다.
비율을 맞춰주는 것이죠.

Classical decomposition 관련해서 실습을 진행한 내용에 대하여 링크를 걸어드리겠습니다.

• 실습 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/classical_decomposition.ipynb
  

지금까지 배운 classical decomposition을 요약하자면 첫 번째로 추세순환 성분 추정시 MA를 이용하기때문에 양끝의 정보손실 문제가 있었습니다. 따라서 불규칙한 성분 추정 시에도 정보 손실이 발생합니다.
두 번째로 급등 또는 급락하는 데이터 기간에 값이 크게 변화합니다. 이것이 평균을 사용하기 때문에 발생하는 이동평균법의 문제입니다.
세 번째로는 계절성분의 값이 주기별로 일정하다는 단점을 갖습니다. 단기간의 계열인 경우에는 합리적일 수 있으나, 장기간의 데이터의 경우에는 적합하지 않습니다.
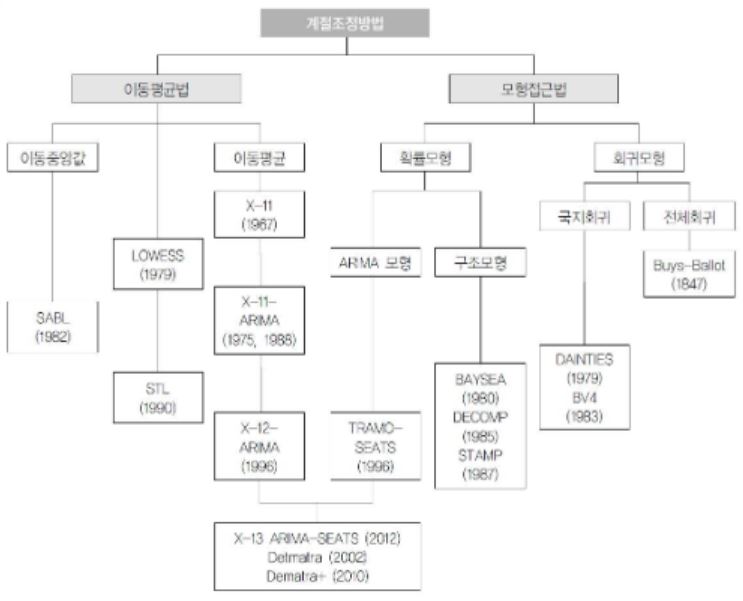
그래서 이러한 한계점들을 바탕으로 다양한 분해법들이 개발되었는데요,
계절 조정하는 여러 방법들이 소개된 사이트입니다.
여기에 링크를 걸어드리겠습니다.

다른 계절 조정방법들 몇 가지만 소개해 드릴텐데요, 미국 Census Bureau와 Statistics Canada에서 개발한 X11 decomposition입니다.
분기와 월별데이터에 자주 사용되는 이 분해법은 앞서 정리한 전통적인 방법의 한계점들을 개선한 모형으로, 추세순환 성분 추정시 관측데이터를 모두 사용하며, 계절 성분이 시간에 걸쳐서 변화하게 됩니다.
휴일 등도 고려하여 예측을 진행하게 됩니다.

R에서는 X11 decomposition을 seasonal package로 제공합니다.

SEATS decomposition은 Seasonal Extraction in ARIMA Time Series의 줄임말로 The Bank of Spain에서 개발되었으며 분기와 월별 데이터만 사용이 가능합니다.
마찬가지로 R에서 어떻게 사용하는지는 아래에 참고하실 수 있도록 이미지를 걸어두겠습니다.

STL decomposition은 Seasonal and Trend decomposition using Loess로 국소회귀를 사용해서 각 변동성분들을 찾는 메소드입니다.
계절주기(월별, 분기 등) 상관없이 활용 가능한 모형입니다. 단 가법 모형에만 적용이 가능합니다.

지금 소개한 건 다 분해법이에요. 추세순환성분, 계절, 랜덤 성분들을 추정해서 예측하는 고전적 방법입니다. 추세 추출 때 이동평균을 썼어요, 근데 꼭 이동평균이아니어도 된답니다.
Classical decompose라는 메소드는 이동평균을 쓴 것뿐이랍니다.
이 모형은 추세순환 성분을 추정하고 추세순환계열로부터 계절성분 추정하고 불규칙성분까지 계산해내는 순서로 진행해줘야하는 것이고요.

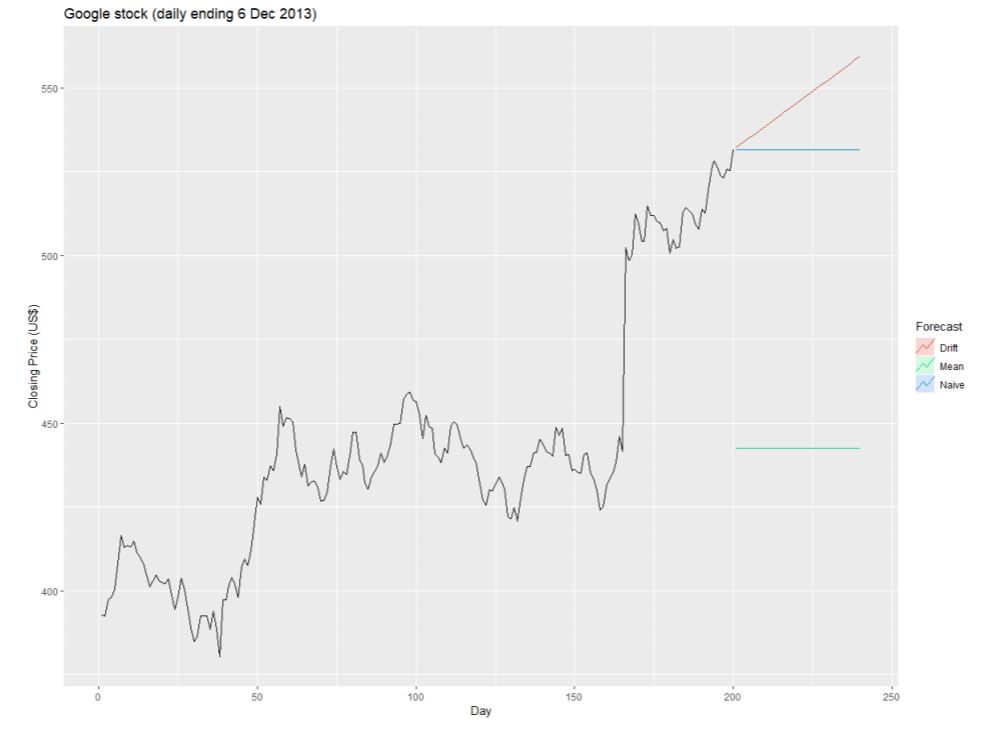
Average method, Naive method, Seasonal naive method, Drift method

오늘은 예측하기 위한 기본적인 벤츠마크를 배웁니다.
통계적 기법이나 머신러닝 기법이 아니라 아주 간단한 기법으로 금융이나 경제 분야에서 많이 사용합니다.
머신러닝 기법이 통계적인 기법보다 좋다 나쁘다하는 총 4가지 기준모형에 대해 배우게 되는데요,
아주 간단하지만, 어떤 때는 아주 막강한 메소드입니다.

1. Average method Meanf(y,h):y는 시계열, h는 미래 시점
   과거 시계열 자료들의 단순평균으로 예측합니다.
   

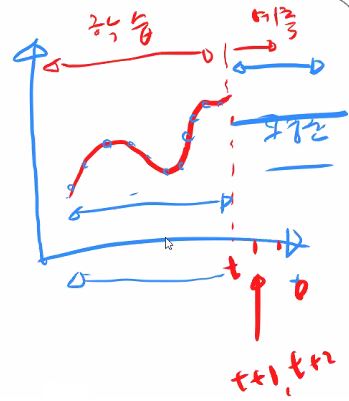
기존까지 배웠던 모형들은 위와 같은 방식으로 예측을 해왔습니다.
T 시점까지 데이터를 두고 그 다음부터는 미래를 예측하도록 했는데, 단순평균법의 경우에는 아래와 같습니다.

1. Naïve method 최근 데이터(관찰값)을 통해 미래를 예측합니다.
   Naïve(y,h) : y는 시계열, h는 미래시점
   전시점을 기준으로 예측하게되는데요
   

그럼 모든 예측값들의 값이 똑같은데 의미가 있나요?
의미가 있을 만한 데이터도 있습니다. 성능이 안좋을 것만 같은 느낌이 몹시 들더라도 이런 메소드들도 있다는 것을 배울 필요가 있습니다.
ses에서 알파가 1일 때 그대로 한칸씩 밀어내는 방식과 동일해요.
t시점으로부터 미래를 예측을하는데 한칸씩 밀어서 예측하는게 아니라 t시점으로부터 끌어오는 것 뿐입니다.

1. seasonal naïve method snavie(y,h) : y는 시계열, h는 미래 시점
   이전 계절값을 사용하는 것은 같으나, m은 계절 기간(the seasonal period)으로 k는 정수(=(h-1)/m)입니다.
   

2. Drift method Rwf(y,h,drift=TRUE) : y는 시계열, h는 미래 시점, drift는 추세
   시계열 데이터의 처음과 마지막 관찰값을 직선으로 연결하는 방법입니다. 즉, 이 메소드의 예측방법은 처음과 끝점을 잇는 직선이에요.
   참고로 드리프트 값이 FALSE이면 naïve method랑 같습니다.
   

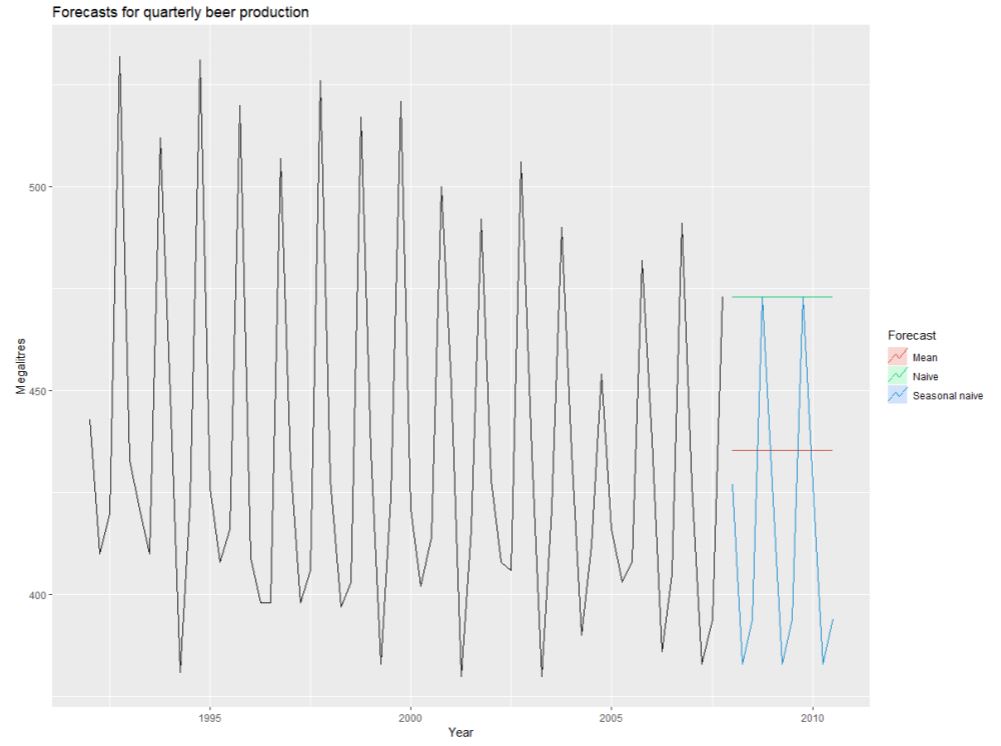
이들을 적용한 예를 살펴봅니다.

이들 메소드들도 이전까지 배웠던 메소드들과 동일하게 학습데이터에 적합시키고 테스트데이터로 예측하면됩니다.

단 파라미터가 없을 뿐입니다.

• 실습1 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/benchmark_1.ipynb
  
• 실습2 보러가기 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/benchmark_2.ipynb
  

이렇게 예측율이 좋지 않은데도 이 메소드들을 사용하는 이유는 무엇일까요?

처음에 소개할 때 썼던 말 “머신러닝 기법이 통계적인 기법보다 좋다 나쁘다하는 총 4가지 기준모형에 대해” 배운다고 했었습니다.

어떤 모형이 좋다 나쁘다는 상대적이므로 적합된 모형 하나만 있을 때 이 모형의 성능이 좋다 나쁘다를 평가하기 어렵기 때문에 오늘 배운 메소드 따위들을 벤츠마크로서 활용하여 (예를 들어 경제데이터의 경우는 나이브모형으로 많이 사용) 적합시켰을때랑 내가 원래 적합시켜놓은 모형의 각자의 RMSE를 비교해주어 이 모형이 좋다 나쁘다를 판단하려는 목적으로 사용되는 것이지요.

머신러닝에서 분류 모형의 기준 정확도는 보통 학습데이터의 종속변수 0, 1 개수로, 학습데이터의 1의 갯수가 90개 0의 개수가 10개라면 90 퍼센트가 기준이 되곤 합니다. 그래서 학습시킬 때 정확도 90 보다 높은 모델을 만들어야 합니다.

비슷하지요?

이처럼 오늘 학습한 방법들을 기준으로 즉 벤치마크로 두고 활용하시면 됩니다. 물론 이 기준 방법이 더 좋다면 예측모형으로 활용하면 됩니다.