ARIMA basics-Time-Series Analysis(2)

Intro

학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.

본 수업에서는 R 언어를 통해 1변량 시계열 데이터를 분석하고 ARIMA 등의 정상시계열 모형을 이용하여 예측하기까지의 실습 및 이론 수업으로 진행됩니다.

실습 환경 구축으로는 R 스튜디오 설치 정도가 있겠습니다.

ARIMA와 Box-Jenkins

오늘은 시계열 분석법 중 아주 유명한 모형인 ARIMA에 대해 학습합니다.

시계열 모형의 통계이론을 구축하는 Box-jenkins 방법론에 의거하여 정상 시계열 자료를 분석하는 방법에 대해 배울 것입니다.
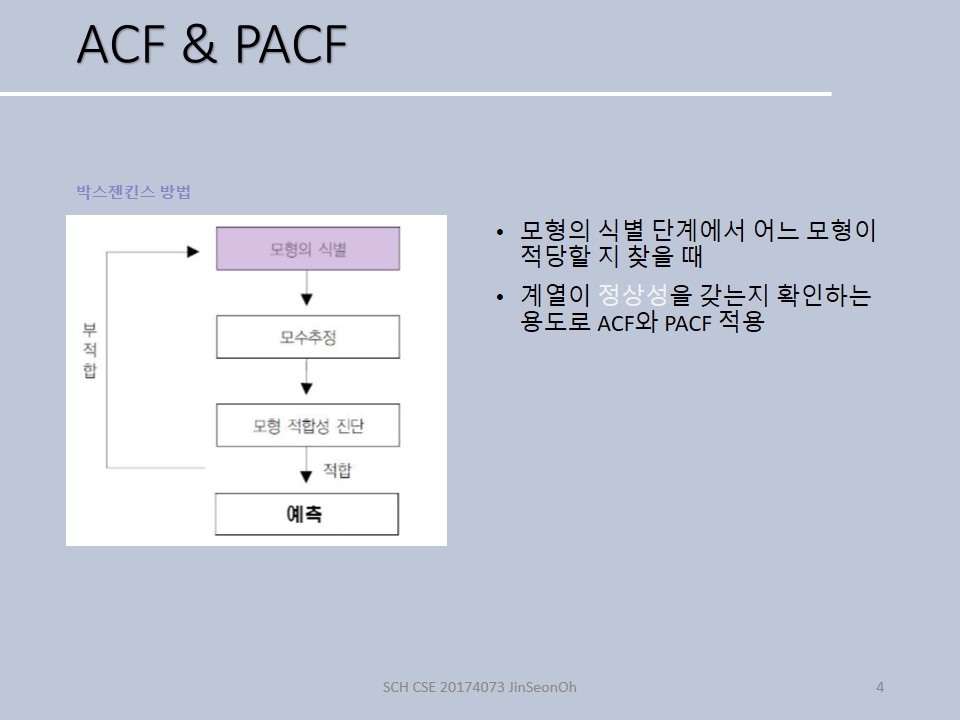
이름에서처럼 Box-jenkins 학자들에 의해서 만들어졌고 아래와 같은 절차를 통해서 모형구축을 합니다.

ARIMA(Autoregressive integrated moving average) 모형은

• AR(파라메터 p)
• MA(파라메터 q)
• ARMA(파라미터 p,q)
• ARIMA(파라미터 p,d,q)
  

이렇게 나눠지게 됩니다.

첫 번째 단계인 모형의 식별은 위 네 가지 중 어떤 모형으로 할 것인지를 결정하는 것을 말합니다.

두 번째 해야 할 일은 모수를 추정합니다.

만약 우리가 AR(p)모형을 쓰겠다 하면 파라메터 p를 추정하는 것을 말합니다.

예를 들어 기계학습 모델에서 회귀분석 모형의 hypothesis인 y=ax+b에서 a, b를 추정하죠? 이처럼 파라메터(모수)를 추정하게 됩니다.

세 번째는 적합성 진단인데, 여느 때처럼 잔차 측도를 기준으로 적합한가에 대한 정도를 평가합니다.
잔차 평가가 우수했다면 해당 적합된 모형을 가지고 이제 예측을 시행합니다.

부적합할 경우에는 모형의 식별로 돌아가는 것이구요.

ARIMA 모형의 박스젠킨스 방법론의 절차를 대략적으로 확인해보았는데 자세히 살펴보겠습니다.

1. 모형식별(identification)
   주요 모형 후보군 도출하는 단계로 자기상관(autocorrelation) 함수와 편자기상관(partial-autocorrelation)함수를 활용해 그 모양새를 보고 어느 모형을 사용할 지 선택합니다.
   

2. 모수 추정(estimation)
   고른 모형의 파라미터를 추정합니다. 최소제곱법, 최대우도법을 자주 사용합니다.
   

3. 적합성진단(Diagnosis)
   잔차 히스토그램 확인 및 통계 검정을 통해 쓸만한 모형을 추려냅니다.
   

4. 예측(forecast)
   추려진 모형으로 예측을 시행합니다.
   
   

사전지식

그런데 ARIMA 모형을 사용하기 위한 기본적인 조건이 있습니다.
바로 정상성이라고 이야기하는 특성을 갖는 시계열자료만을 ARIMA로 분석할 수 있습니다.

ARIMA 모형을 이해하기 위한 기초 주요개념이 있습니다.
확률과정과 정상성(Stationary Process)에 대한 개념부터, 자기공분산함수, 자기상관함수, 편자기상관함수, 백색잡음(white noise)이나 확률보행과정(random walk) 등이요.

차근차근 알아봅시다.

가장 먼저 시계열이라하면 시간 순서를 고려하여 관측된 y 값들이 찍히는 것을 말합니다.

실제 관찰된 자료는 확률변수 Zt의 모집단으로부터 각 시점에서 얻어진 표본이 됩니다.

각 시점에서 표본이 하나 얻어져서 실현되었다라고 말하기도 합니다.
그래서 실현값(realization)이라고도 부르는데, 이러한 확률 변수들의 집합을 확률 과정이라고도 합니다.

시계열의 특성을 살펴보는 기술적 척도는 평균, 분산, 자기상관성 등으로 측정합니다.
시계열이 그러한 확률적 구조를 갖고 있다고 보는 거죠.

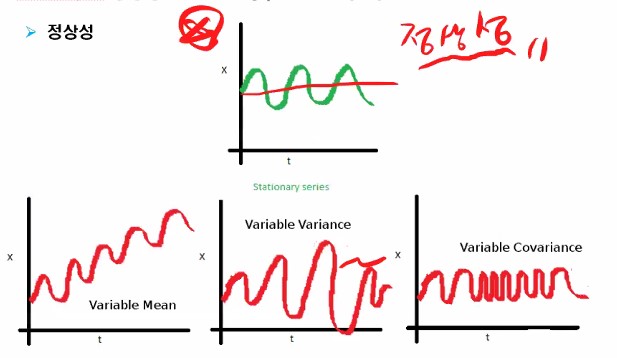
그 다음 중요한 개념이죠, 바로 정상성(stationarity)입니다.

이러한 특성은 시계열의 확률적인 성질들이 시간의 흐름에 따라 불변한다라는 것인데요, 따라서 정상성을 가진 시계열의 경우 뚜렷한 추세가 없습니다.

어려운 말을 쉽게 풀어 설명하자면 시간축과 평행하게 시계열의 평균이 나타나게 된다라는 것을 말합니다. 추세가 있지 않습니다.
시계열의 진폭(변동) 역시 시간의 흐름에 따라 일정합니다.
다른 말로 분산이 일정하다고도 표현합니다.

저 초록색과 같은 데이터가 이상적인 정상 데이터의 형태입니다.

아래의 첫 번째 계열은 평균이 일정하지 않고, 두 번째 진폭(분산)이 일정하지 않고, 세 번째의 경우를 보면 평균도 일정하고 진폭도 어느 정도 일정하나 간격, 주기의 변화가 있죠?
이런 경우도 정상성을 갖는 것이 아닙니다.

참고로 세번째 경우에는 공분산이 시차 k에만 영향을 받아야 하는데 시점t에도 영향을 받기 때문입니다.

위 세가지 데이터들을 비정상성(non stationary) 데이터라고 이야기할 수 있습니다.

그럼 ARIMA 모형은 당연히 위에 초록색 모형만을 사용할 수 잇겠죠?

너무나 제한적인데 이거 써먹을 수 있을까요?

네! 비정상 원본 데이터를 정상성을 갖도록 변환해주면 됩니다.
보통은 차분을 한다거나 루트를 씌운다거나 로그를 씌워서 정상성을 갖도록 변환해준답니다.

그래서 탐색적 데이터 분석(EDA)를 하기 위해서 원본데이터를 꼭 찍어봐야만 합니다.

변환 시켜주는 것은 다음에 이어서 쓸 것입니다.

정상성에도 강한 정상성이 있고 약한 정상성이 있습니다.
우리가 다루는 데이터는 모두 약한 정상성을 갖는 데이터로만 실습해볼 것입니다.

약한 정상성이란 평균 값이 일정합니다, 즉, 시점 t에 의존하지 않습니다. 즉 시점이 바뀌어도 평균이 일정하다는 것이죠.
분산도 시점 t에 의존하지 않습니다.
Zt와 Zt+k간의 공분산과 상관 함수는 단지 시차(lag) k에만 의존하고 시점 t와는 무관합니다.

이 세가지 특징을 기억해주셔야합니다.

특히 세번째 특징이 중요한데요.
하나의 시계열 데이터를 Z라고 합시다.
Zt+k나 Zt-k여도 되요.
여기서 말하는 공분산, 상관함수(correlation)는 꼭 시계열이 아니더라도 키,몸무게 feature에 대한 음의 상관관계를 갖느냐, 양의 상관관계를 갖느냐 하는 문제하고 똑같아요.

시계열 데이터를 가지고 시차 k만 가지고 상관계수를 구하고 싶은 것입니다.
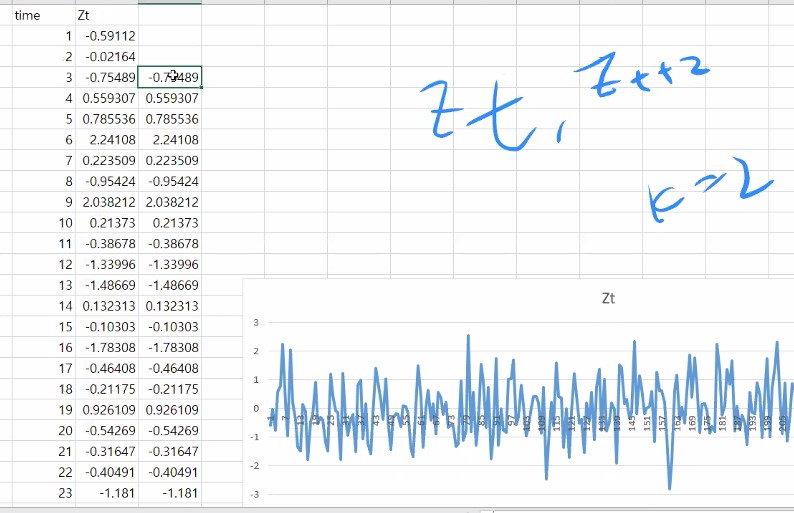
(Zt,Zt+2) 이런식으로 데이터들을 가지고 상관함수에 넣으면 그게 자기 상관성을 보는 것이 되는 거에요.
그렇게 하게되면 시차 k는 2겠죠?

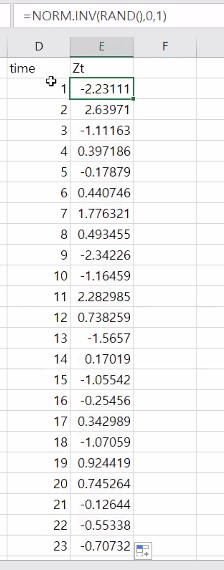
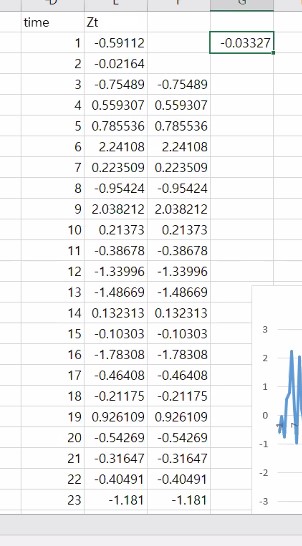
이거는 상관함수 예제를 보기 위해서 엑셀로 직접 제작한 랜덤 시계열 데이터 입니다.
가장 밑에 있는 게 최근 데이터라 합시다.

Correlation 함수를 쓰죠.

다시 말해 Zt 하고 Zt+2간의 상관관계를 보기 위해서 correleation 함수를 쓸 것인데 Zt든 Zt+2든 한 계열에 대한 정보죠?

자기 상관함수를 보기 위해서 하나의 데이터를 써줘야해요.

-0.03327 이 시차 2에 대한 자기 correlation()의 값입니다.
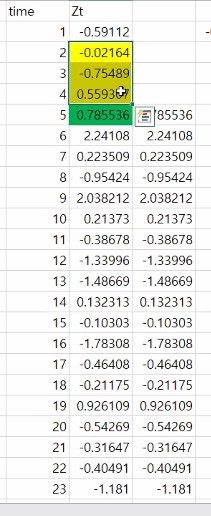
참고로 상관계수는 공분산을 X변수의 표준편차*Y변수의 표준편차로 나눠주는 것을 말합니다.

우리는 데이터 가지고 공분산 구하고 상관계수값을 구하는데 이 앞에 자기라는 말을 붙이게 됩니다.
자기 공분산, 자기상관함수 이런식으로요.

약한 정상성에는 t랑은 상관없이 시차 k에 만 의존하여 공분산과 상관함수가 결정됩니다.

실제 수식들은 위와 같습니다.
그냥 이변량 데이터가지고 계산하는 것과 똑같아요.
자기공분산->자기상관함수 그저 표준편차로 나눈 것이죠?

표본 샘플 자기 상관함수는 말 그대로 데이터 샘플 추려와서 계산한 것을 말합니다.

더 자세히 알지 않아도 문제를 해결할 수 있습니다. 이런 게 있다 정도만 알면 될듯합니다..

한 가지 더 편자기 상관함수에 대한 개념도 배워봅시다.

이건 좀 어려울 수 있어요.
자기 상관계수 계산과 비슷한데,

시차가 4라고 합시다. 시차 k에 대해서 그 중간에 끼어있는 숫자들의 상호 의존성을 제거하고 거기에 해당하는 값들로 계산이 되는데 편자기상관의 경우에는 중간에 있는 영향을 미치는 것들을 없애고 계산한 값을 주는 함수다까지로만 이해하고 넘어가도록 합시다.

여기까지가 ARIMA의 첫 번째 조건인 정상성 데이터여야 한다! 를 배운 것입니다.

모형의 식별

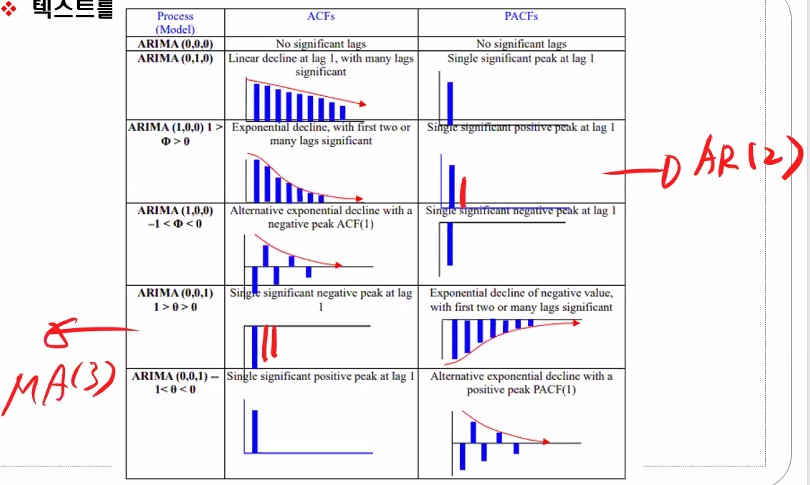
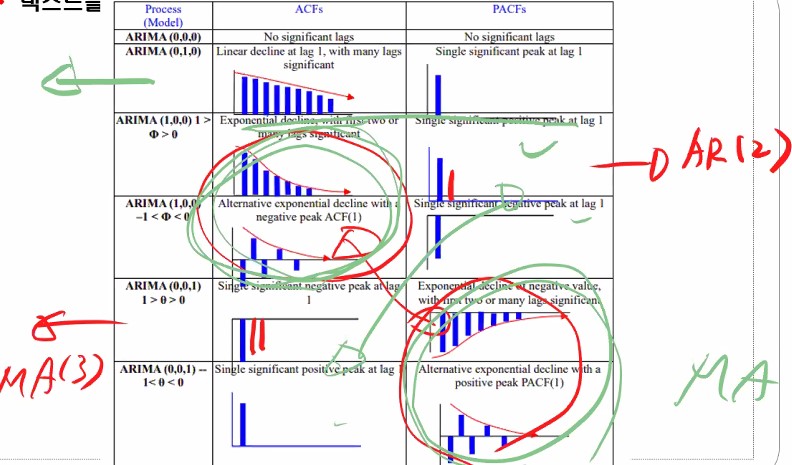
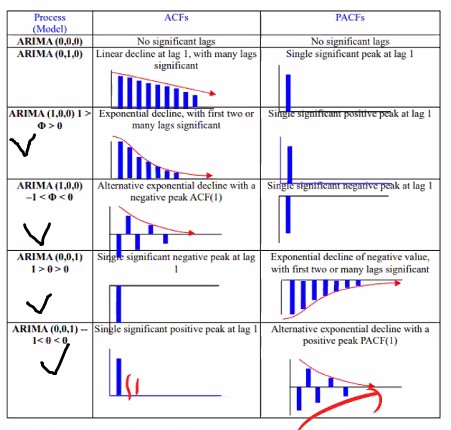
박스 젠킨스의 첫번째 방법인 모형의 식별 단계에서 방금 배운 개념인 자기상관함수(Auto Correlation Function)와 편자기상관함수(Partial Auto Correleation Function)를 가지고 모형을 식별하게 됩니다. 무슨 말인지는 아래 설명을 보시면 이해하실 수 있을 겁니다!
ARIMA는 이 그래프들만 이해할 수 있으면 사실 끝이에요.

코렐로그램(correlogram)이라고 불리는 표입니다.

옆에 보면 process라고 써있는데 그냥 모델을 말합니다. 어렵게 생각할 필요 없습니다.
Staistical terminology를 사용하다 보니까 process라고 써놓은 것 뿐이에요.

ARIMA(p,d,q) 였죠.
첫번째 p는 AR에 들어가는 파라미터로 시차k에 해당합니다.

p==1일때는 Yt = α Yt-1+1이라면, p==2일때는 Yt = α Yt-1 + α Yt-2 + 1이 됩니다.

d는 차분을 말합니다.
전시점에서 오늘 시점꺼를 빼서 데이터로 이용하는 건데, 그 차분값 1이면은 한번만 빼기를 시행하며 1차차분이라 부릅니다.
차분값이 2면 두 번 빼기를 시행하고 2차차분이라고 불러요.

q는 MA모형에 들어가는 차수로 몇 개의 전데이터 또는 전전데이터 가 들어가는가에 대한 의미에요.

그림에 나와있는 첫 번째 ARIMA(000)은 아무것도 아니에요.

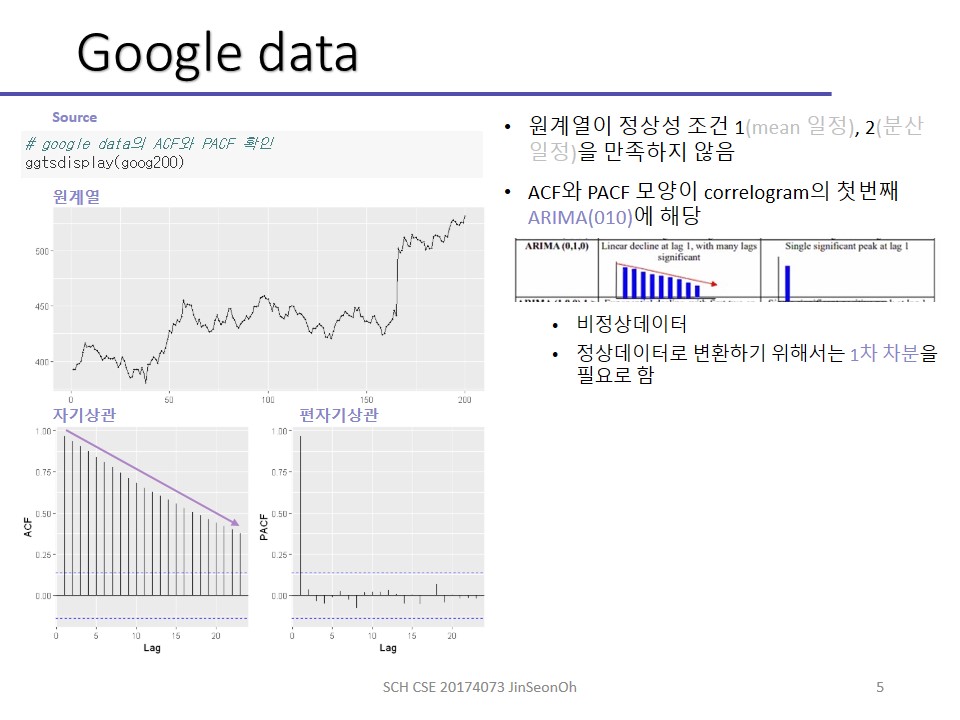
원본 데이터에 대해 ACF(자기상관함수) 하고 PACF(편자기상관함수)를 적용해서 그래프로 표현이 되면은 위와 같은 형태들 중 하나로 나오게 될겁니다.

이 값은 우리가 실습을 좀이따 하겠지만 요런식으로 나옵니다.

가로축은 k값 시차를 말합니다.

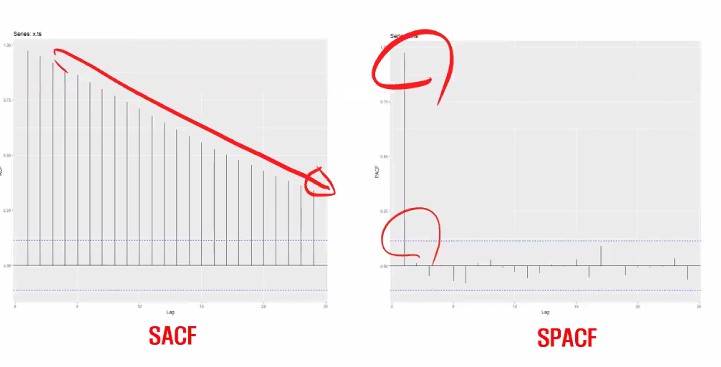
다시 correlogram으로 돌아와서 000을 제외하고 010을 봅시다.
1차차분하라는 거죠?

데이터의 특성이 ACF를 그려보고 PACF 그려봤더니 저렇게 그래프가 나왔다, 대각선으로 선형적으로 줄어드는 형태이고 PACF는 하나만 툭 튀어나왔다라면 1차차분을 하라는 거에요.

코렐로그램상에서 그 다음 것도 봅시다.
ARIMA(100)쪽을 보면 ACF 모형이지수적으로 감소하는 형태이죠? PACF는 하나만 크게 나와있죠?

이렇게 나오는 경우는 AR1 모형을 선택하는 것이 적절하게 선택한 거에요.

그 밑에 것도 파라메터가 똑같죠. 양측으로 드러난 것일 뿐 지수적으로 감소합니다.
PACF는 하나가 아래로 나와있죠.
계수값 크기에 따라서 모형이 바뀌어요.
ARIMA(1,0,0) 모형은 AR모형이라고도 부릅니다.

이번엔 MA를 봅시다.

얘네는 MA(1)이죠. 앞에서 배운 MA가 아니에요. 그건 잠시 머리 속에서 떼어둡시다.
PACF가 어떤가요? 아까 AR에선 ACF가 줄어들었는데 MA에선 쟤네들이 지수적으로 감소하죠?
대신 ACF가 한칸 튀는게 나오는 것을 확인하실 수 있습니다.

이런 식으로 ACF와 PACF 그래프를 그려보고서 ARIMA중 어느 모형을 쓸지를 결정 해야 해요..

지금은 한 칸이지만 두 칸, 세 칸이 튈 수 있어요.
그들로 파라메터의 차수를 결정할 수 있습니다.

그럴 땐 그림처럼 저렇게 나온다고 보시면 됩니다.

어쨌든 재밌는 건 AR모형하고 MA 모형의 그래프가 반대? 대칭된다라는 것입니다.

(000을 제외하고서) 첫 번째 데이터는 ‘이 계열은 비정상데이터이니까 1차차분을 하렴’이라는 뜻이 됩니다.

대부분의 데이터들은 1차 차분을 하면 정상성을 유지하곤 합니다.

여튼 그래프를 보고 어느 모형을 쓰며 차수를 어떻게 할 지를 결정하면 된다고 보시면 됩니다.

위 그래프를 뭐라 부르냐면 자기상관성도표(correlogram) 코렐로그램이라고 부릅니다.

이미 forecast 패키지 안에 이들을 볼 수 있는 함수들이 구현되어있습니다.

마지막 함수ggtsdisplay()를 호출하면 쟤네들(원계열~pacf)을 동시에 표현해주게 됩니다.

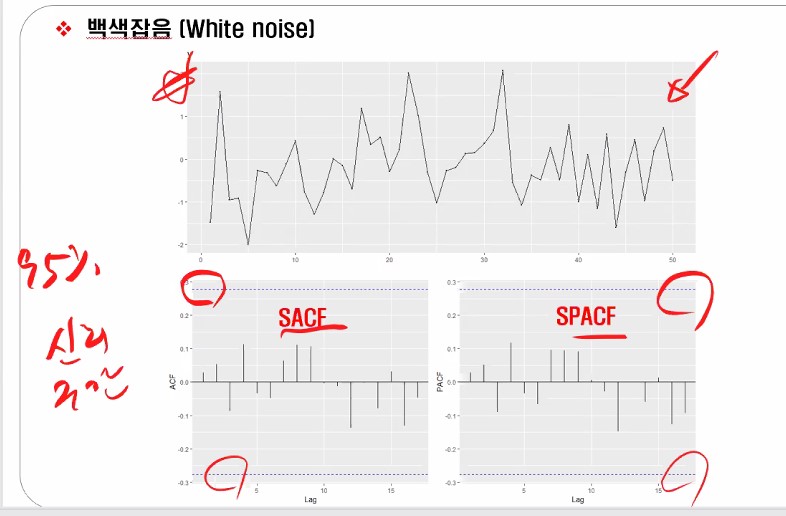
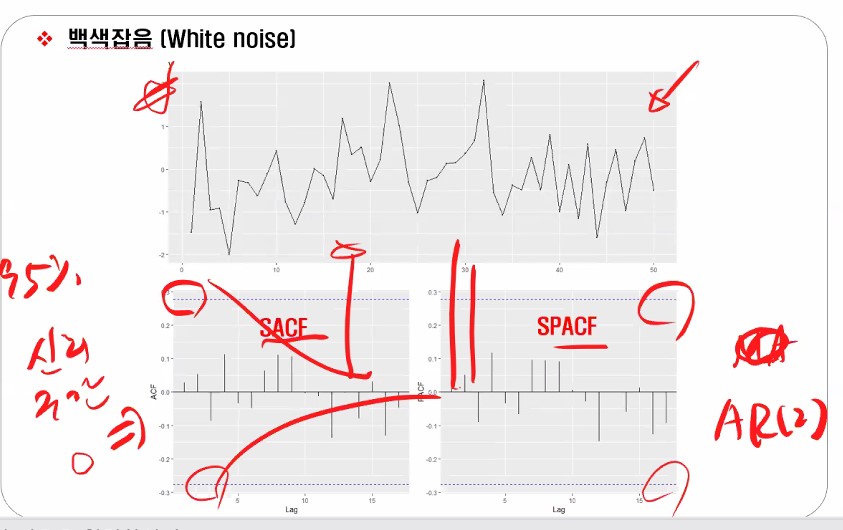
백색잡음(White noise)

추후에 보게되겠지만 arima 모형식에서의 입실론에 해당하는 term을 백색잡음에 해당하는데요,
데이터들 IID 형태로 평균이 0이고 분산이 일정한 데이터는 백색잡음이라고 부릅니다.

Rnorm 정규분포 형태의 데이터 50개를 만들어주고 어떤 데이터가 편자기 상관함수랑 자기상관함수로 나오는지 실습을 해보겠습니다.
실습 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/White_noise.ipynb

저 파란 점선 부분이 신뢰구간인데 치고 올라가야 값이 나왔다고 인정할 수 있는 거에요.

이렇게 될 때 AR(2)가 되는 거구요.

근데 지금 나온 걸 보면 튀긴 튀지만 신뢰구간 안에 있죠?
한 번 더 보여드리자면, 파란색을 벗어나서 튀어야 튄 걸로 인정이 됩니다.

이런 식으로요!
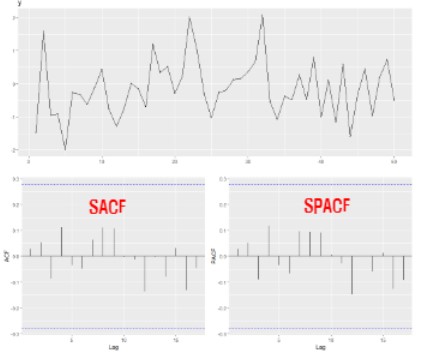
참고로 이렇게 나오면 차분해야겠죠?
왜냐하면 코렐로그램에서 ARIMA(010)에 해당되는 SACF와 SPACF 형태를 보이고 있으니까요!

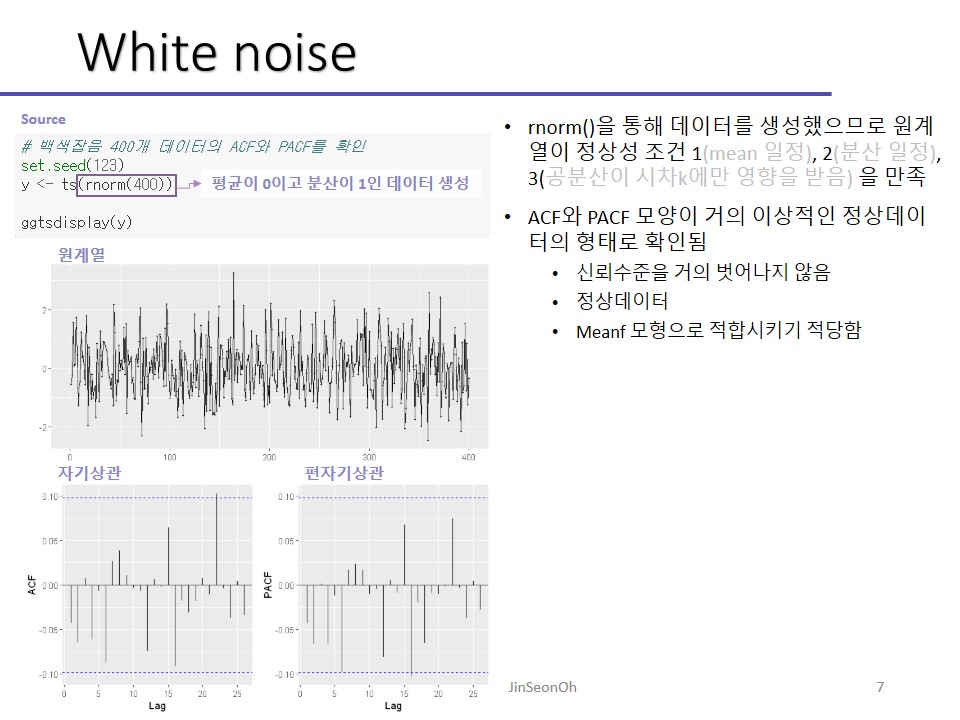
어쨌든 좀 전에 실습에서 만든 게 정규분포데이터 만들어서 시계열로 만든 거에요. rnorm 평균이 0이고 분산이 1인형태로다가요, 분산이 1로 일정하다고 가정한 거에요.
정상성이라는 개념자체가 평균이 일정하고 분산도 일정한 형태니까요.

데이터 자체를 rnorm을 써서 뽑아온거죠.
평균이 0이고 분산이 1일 것을 만족하는 데이터로만 나왔을겁니다.
그러니 당연히 정상성을 만족하는 데이터로 나왔을 겁니다.
자세히 보면 첨에 엑셀에서 만들어준 데이터도 그랬어요.

백색잡음이라는 것은 즉, 정상성을 설명할 때 확률과정들이 서로 독립이고 동일한 분포를 가지며 평균을 일반적으로 0으로 가정하며 분산도 일정하다라는 말을 하고 있네요.
아주 강한 정상성을 띄는 것이라고 말씀드릴 수 있습니다.

또한 더불어 정상성이라는 것은 시차k간의 공분산은 0으로 시간 t에 의존하지 않는다는 것을 알고 계시면 됩니다.
이러한 특징을 가져야만 정상성을 만족시키는 데이터라는 것을 아시면 됩니다.

시차에 차이가 없으면 즉 k=0이면, 백색잡음과정에서는 자기상관함수는 0, 편자기도 0이나오는 형태라고 확인할 수 있습니다.

다시 돌아와서 원계열을 보시면 평균 0이고 분산 일정한 형태의 원본데이터 확인되시죠.

아까 실습 이후에 파란색(신뢰구간) 안 넘어가면 다 0으로 취급하기로 했죠?

그렇다는 것은 백색잡음데이터들은 서로 연관이 없다고 말할 수 있는 것이고, 그래서 정상성을 가진 데이터라고 가정할 수 있는 것이죠.

나중에 잔차 검증 때 서로 영향을 미치는지 안 미치는 지 따로 확인할거거든요?

그 때 가서 더 배우겠지만, 잔차가 백색잡음처럼 나와야해요!
예측오차값들도 백색잡음 형태로 나와야 적합한 모형을 썼다고 평가할 수 있는 거에요.

좀 전에 해봤던 실습이 그 백색잡음을 한번 실습해본 거에요

확률보행과정(Random Walk Process)

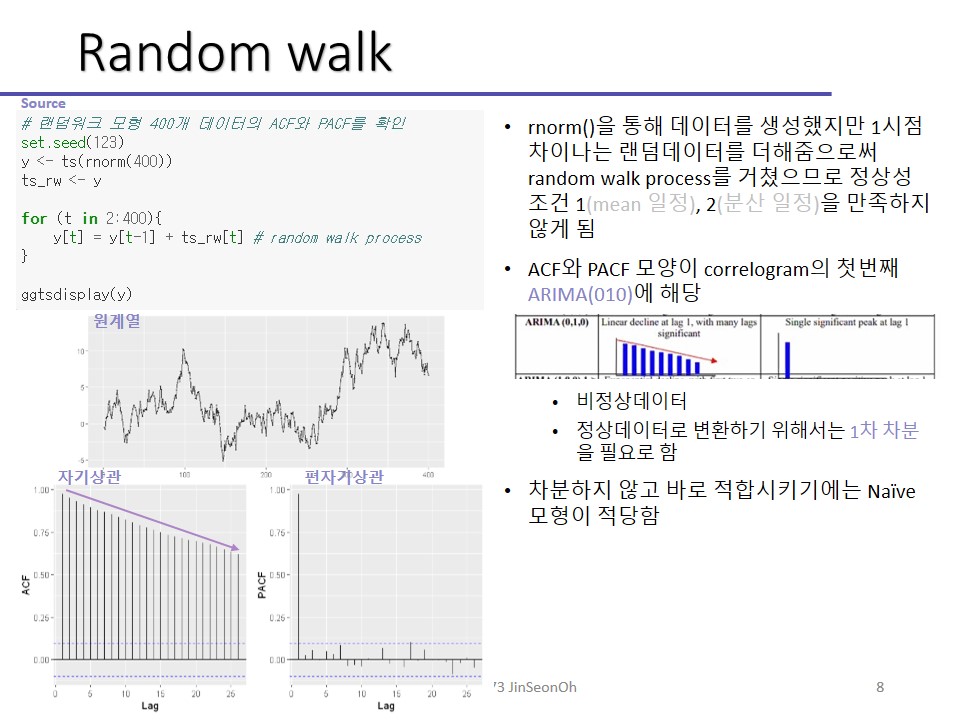
그 다음 확률보행과정(random walk process)에 대해 배웁시다.
이름에서 드러나듯 술 취한 사람이 어디로 갈지 모르는 것처럼 대표적인 불안정 시계열 확률과정입니다.
Zt = Zt-1+ εt로 정의됩니다.
이 때 ε 은 아까 잠시 설명했던 것처럼 백색잡음에 해당합니다. 그래서 식을 해석하면 전시점의 데이터 + 백색잡음입니다.

실습 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Random_Walk_Process.ipynb

아까 백색잡음하고는 ACF와 PACF가 다르게 나왔죠?
백색잡음의 ACF와 PACF 모형, 그 다음 확률보행과정의 ACF와 PACF 형태를 잘 기억해두시는 것이 좋습니다.

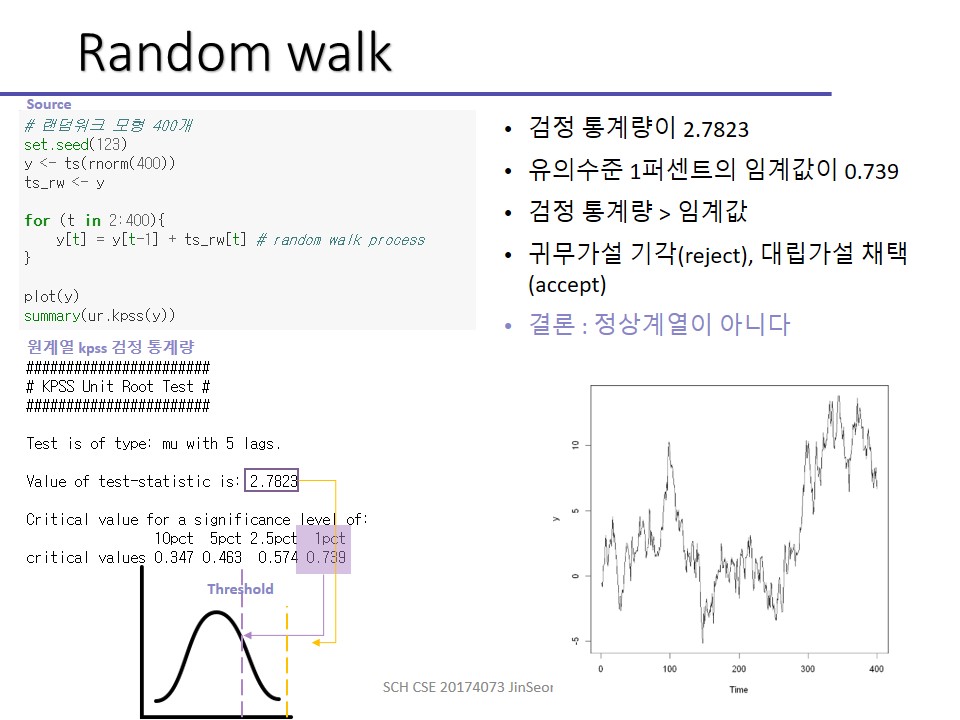
지금 해본 실습은 랜덤워크에요.
랜덤워크는 대표적인 비정상 계열이에요.
처음에 봤던 그 차트에서 ARIMA (010)에 해당하지요? ACF는 선형적으로 감소하고 PACF는 하나가 튀어나왔으니까요!

참고로 분석을 할 때는 조금 튀어나오지 않았나? 이렇게 빡빡하게 기준을 세우기보다는 융통성 있게 봐야 해요!
교묘하게 지수적으로 감소했다고 하면 안돼구요..ㅎㅎ

즉 비정상데이터를 정상데이터로 바꿔주기 위해서는 차분! 해야 한다는 말을 하는 거고요

또는 첨에 말한 것처럼 루트나 로그 씌우기 등의 방법도 있습니다.

랜덤워크 프로세스 데이터 시드값을 고정안하고 다시 돌려보게 되면 또 다른 모형이 나올 거에요 계속 반복적으로 돌리다보면 이러한 특성이 마치 주식데이터와 비슷하다는 것을 알 수 있습니다.

주식데이터 흐름하고 유사하게 나오는 경우가 있어요.
주식데이터는 랜덤이라고 나와있지만 자꾸 많은 사람들은 예측하려 들지요 ㅎㅎ.
사실 예측이 불가능하다고 말할 수도 있는 건데 말이에요.

다음 시간에는 차분하고, 로그 씌워서 비정상->정상으로 변환시키는 과정을 보고 모형 별로 AR, MA,ARMA, ARIMA할겁니다.

시간이 된다면 SARIMA까지 볼 거에요
S는 seasonal입니다.

여태 앞서 배웠던 모든 모형들 전부 SARIMA면 다 커버됩니다.

나중에 Neural Network로 시계열 다루는 것까지 할거에요.!!

ARIMA를 잘 사용하기 위해서는 앞에서 봤었던 코렐로그램을 꼭 기억하고 있어야 합니다.

화이트 노이즈와 랜덤워크 실습에서처럼 ACF와 PACF가 어떻게 나오는지를 봐야 해요.

백색잡음은 0에 해당하는 값이 나오니까 아무런 영향을 갖지 못합니다.
시계열 간에 영향이 없습니다.

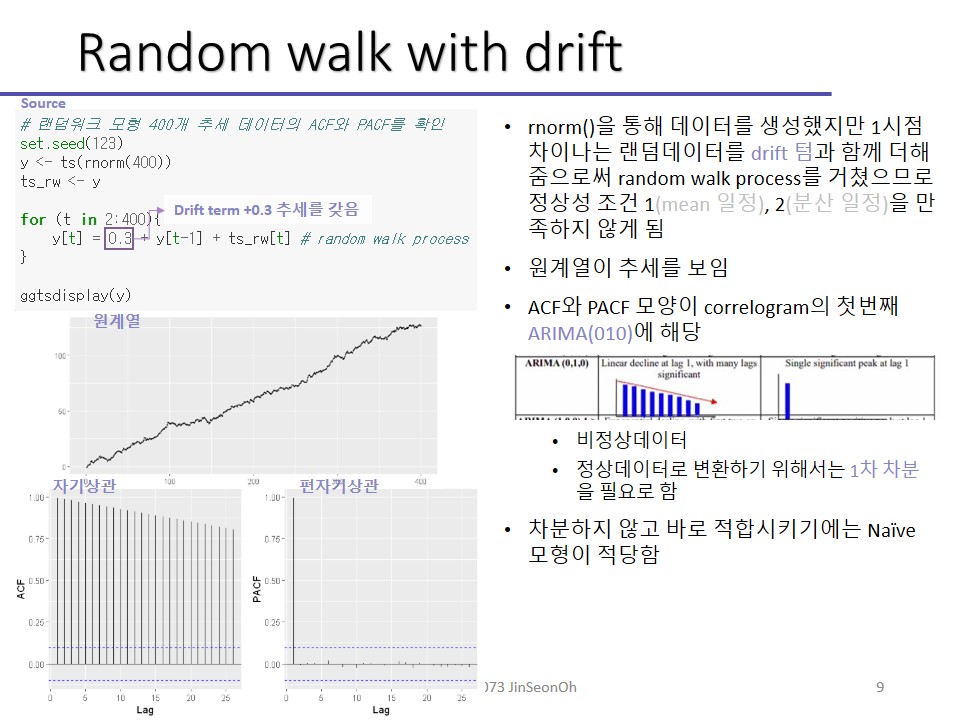
Random Walk with drift term

랜덤워크를 통해 대표적인 주가그래프 형태를 볼 수 있다고 확인할 수 있었습니다.
현재 시계열 데이터는 전시점 데이터에 입실론을 더 하는 것이라고 수식에 드러나있었던 것 기억하시나요? 그리고 거기에서 입실론이 바로 화이트 노이즈에 해당하는 것도요.

Zt = At-1 + εt, Zt-1 = Zt-2 + εt-1…. 이렇게 구해가야 하니까
Zt = Zt-2 + εt-1입니다.

계속 재귀적으로 입실론을 더해가는 형태니까 구하기가 쉽지 않습니다.
결과적으로 초기값 E부터 계속 더해가는 과정이 되겠지요.

분산은 선형결합형태로 나오고 있죠. 0~1사이의 분포를 갖고 있고, 공분산 역시 분산과 같은 형태를 갖게 됩니다.

약한 정상성의 조건이 있었죠. 평균이 일정하고 분산도 일정하고 공분산도 시차k에만 의존적일 뿐 시점 t와는 상관이 없다. 였습니다.

랜덤워크는 분산 평균은 일정하지만 공분산이 t에 영향을 받죠?
그렇기 때문에 대표적인 비정상성 데이터 입니다.

선형회귀 Y = ax + b 식에서 b가 절편입니다. b를 drift term이라고도 부르죠.

사실 시계열은 회귀분석과 비슷해요.
변수 x없이 y가 들어가면서 Y= aY + b 로 바뀌고 자기회귀가 되는 것뿐입니다. Auto Regressive 모형이지요.

어쨌든 식에서 랜덤워크의 계수값이 1이라는 것을 기억해줘야 합니다.
그럴 때 랜덤워크 프로세스라고 이야기할 수 있는 것입니다.

앞의 계수값이 -1에서 1사이의 값이라면 AR모형이 됩니다.

참고로 절편이 있는 경우엔 식을 보면 δ(델타)라는 텀이 붙습니다.

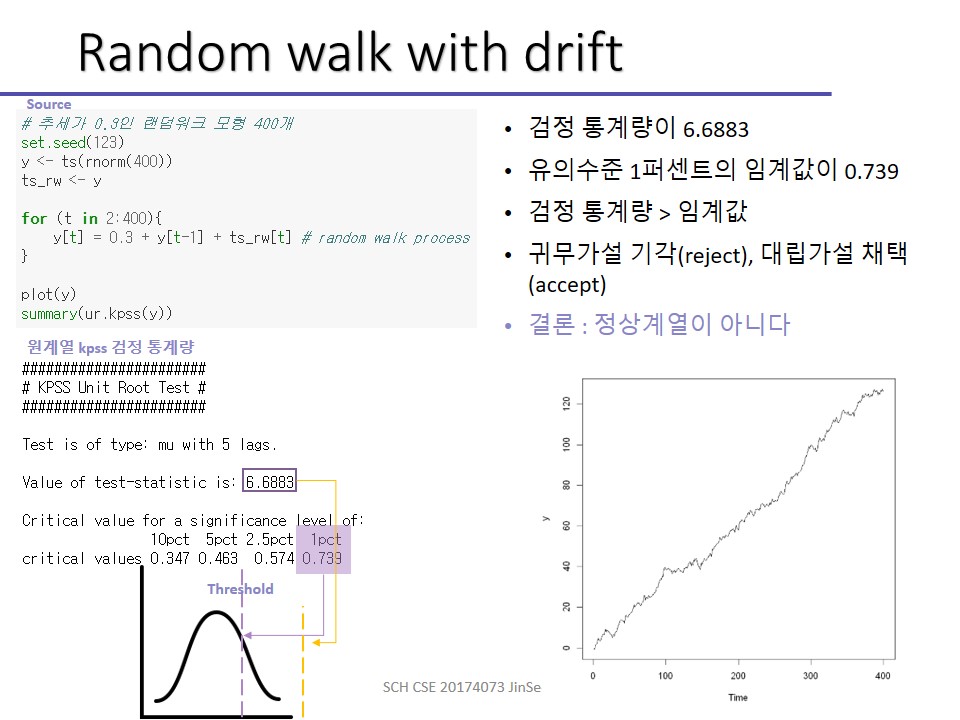
앞서서는 절편이 없는 경우를 한번 해봤죠. 주가 형태를 띈다는 그 그래프요.
이번엔 0.3, -0.4로 차례로 drift텀을 이용해보겠습니다.

그래프를 그려 체크해보겠습니다.

실습 링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Random_Walk_drift_term.ipynb

절편이 있는 건 드래프트 텀으로 방향성을 잡아준다고 볼 수 있습니다. 추세가 있다는 것을 알 수 있습니다.

지금 배운 랜덤워크의 경우는 대표적 비정상 시계열을 내게 되는데, 그렇다는 것은 AR모형을 쓸 수 없다는 뜻이지요.
바꿔줘야 해요. 어떻게 할까요?

Zt - Zt-1 = εt로 이항시키면 됩니다.
화이트노이즈는 굉장히 강한 정상성을 가진 형태를 내므로 가능해지는 것이죠.

이 과정을 차분이라고 말합니다.

Drift term을 두는 경우에도 차분하면 우변에 d_term + εt만 남게 되며, 이 때 d_term은 상수이므로 차분을 통해 정상성을 갖는 것이 가능해집니다.

그 데이터의 분포를 봤을 때 상승세를 보이거나 하락세를 보였었죠? 추세가 있는 데이터는 차분을 하면 정상 시계열로 될 가능성이 큽니다.

R에서는 diff()함수를 사용해주면 차분됩니다.
이렇게 차분한 데이터를 가지고 모형식별, 모수추정 등에 이용하는 거에요.

다만 예측을 하려면 차분했던 데이터를 다시 원래 데이터의 시계열로 환원시켜줘야겠죠?

어차피 R을 쓰면 자동으로 해주긴 합니다. 원리 정도만 알아둬도 돼요.

단 정상성 데이터로 어떻게 변환을 해줘야 하는 가는 알아야 한다는 것이죠.

실습 링크 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/Random_Walk_to_Stationarity_Series.ipynb

그 다섯 가지 모형에서 첫 번째가 나와서 1차차분을 했는데, 그러고 나서 나온 형태를 보니까 ARIMA(000)의 형태가 나왔거든요.

그럼 이럴 땐 어떤 모형으로 예측을 해주는 것이 좋을까요?
평균이 일정한 형태니까 meanf()를 쓰는 것도 좋을 것 같습니다.

그럼 백색잡음은 meanf 모형을 쓸 수 있다를 알았고,
확률보행과정 형태의 데이터를 봤을 때는 어떤 모형을 쓰는 것이 좋을까요?

시계열에서는 현재시점의 데이터는 모든 과거 정보를 다 포함하고 있다. 라는 가정을 가지고 있는 거에요.
그러니까, 제일 마지막에 나온 데이터가 모든 정보를 다 포함하고 있다고 생각하는 거죠.

직전 데이터만을 가지고 예측을 하는 모형이 있었죠? naive입니다.

자 아래 아홉 가지 시계열자료를 보고 ARIMA에 쓸 수 있을지를 판단해봅시다.

첫번째는 X요. 평균이 일정하지 않고 추세를 갖죠.

두번째는 O에 가깝습니다. 하나쯤 튀는 것에 대해서는 융통성을 어느 정도 두고 보는 것이죠

세번째는 애매모호하네요. 조금 더 많은 데이터가 있었다고 하면 판단하기에 더 좋겠는데, 아마 분산도 위아래로 일정하게 나온다는 것을 기대하고 O에 한 표 하겠습니다.

E는 확실히 아니죠. 정상계열은 계절성이나 추세를 가질 수 없습니다.

G는 X라고 하겠습니다.
어느 정도 주기가 보여서요.

교재에서는 DHI계절성을 보인다, ACEFI는 추세성을 보인다, BG 정상성을 보이며, G는 순환변동이라고 설명하고 있습니다.
g와 h 차이라 하면 오랜 기간에 걸쳐 주기가 보여서 g는 순환, h는 비교적 짧은 주기로 계절입니다.

정상성을 갖도록 시계열 데이터를 변환할 때 자주 사용하는 방법은 차분 또는 자연로그가 있습니다.

보통 차분은 평균의 정상화를 위해 많이 사용되며, 자연로그는 분산의 안정화를 위해 많이 사용됩니다.

실습링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/stationary_series_diff,log.ipynb

다음 시간엔 얼마나 비정상 경향이 있는가를 보는 방법을 배울 겁니다. 오늘 배운 것에서 중요한 점은 ACF나 PACF 패턴을 보고 어떻게 모형을 고를 것인지 적절하게 변환할 수 있어야 한다는 점입니다.

정상성 확인과 잔차 평가

오늘은 정상성을 판단하는 방법과 잔차를 따지는 방법을 보도록 할 거에요.

적합 후에 잔차가 어떻게 나오는 지 보는 것도 박스젠킨스 방법 절차에 있었지요?

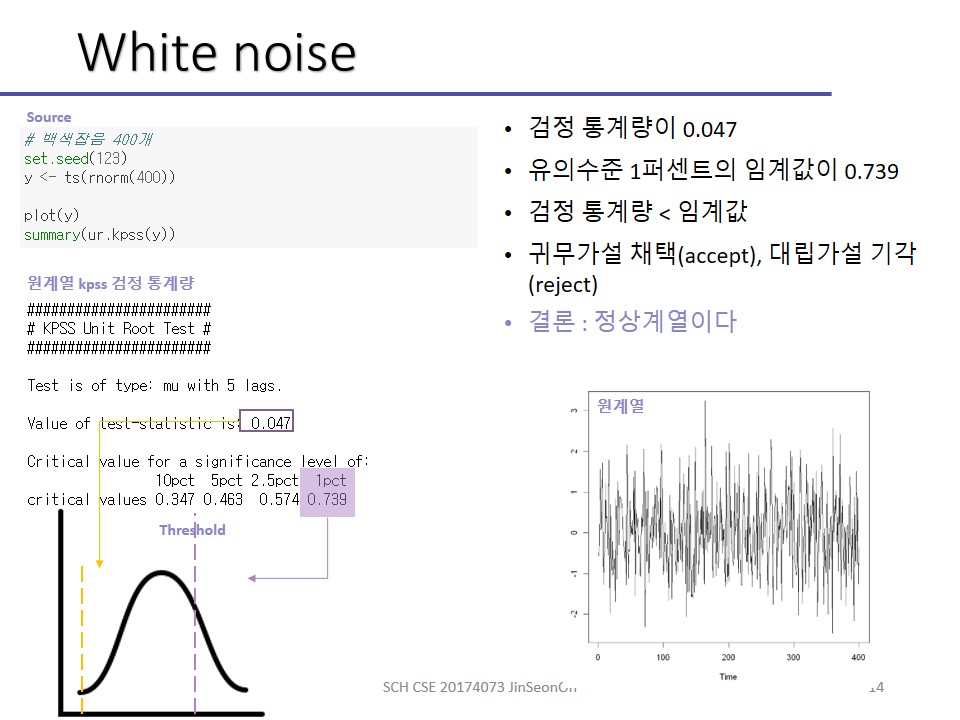
White noise는 대표적인 강한 정상 시계열이므로 meanf 모형을 통한 예측, random walk는 naïve 모형을 통한 예측이 보다 적합합니다.

Random walk에 Naïve 모형을 적합시키고 원계열과 적합된 계열을 차트로 그려보는 실습을 할겁니다.

적합된 모델의 잔차를 평가하기 위해 checkreseiduals(naïve(데이터)) 함수를 활용해보는 것까지 다룹니다.

실습 링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_checkresiduals_of_randomwalks.ipynb

Set.seed(123)로 두고, 400개 데이터 생성을 통해 랜덤워크과정을 보이고, 잔차를 평가했는데요.

히스토그램을 보면 정규분포를 이루며 잘 적합된 것처럼 보입니다.
ACF는 왜 보여준걸까요? 시계열데이터다보니까 ACF까지 한번 더 보는거에여. ACF 함수가 앞뒤 시차간의 간격끼리 연관이 있는지 없는지를 모아놓은 그래프니까요!
0이어야만 잔차평가가 우수한 것입니다.

위 실습에서는 추세가 있는 데이터도 함께 실습해보았습니다. 드리프트 텀을 가진 random walk 지요.

정상시계열인지를 판단하는 방법으로는 여러가지가 있습니다.
첫 번째는 ACF함수를 이용하는 방법입니다.
ACF는 원계열의 정상성 뿐 아니라 위 실습에서처럼 잔차 평가에도 활용할 수 있습니다.

두 번째 시계열이 정상시계열임을 판정하는 방법으로는 통계적 검정을 통한 방법입니다.

원계열, 잔차 검정에 활용 가능한 Ljung-Box 검정과 KPSS(Kwiatkowski-Philips-Schmidt-Shin test) 검정이 있습니다.
참고로 KPSS는 단위근 검정(Unit Root Tests)법 중 하나입니다.

저희 수업에서는 Ljung-Box를 잔차 검정에 활용하고 KPSS를 원계열 검정에 활용하겠습니다.

통계적 검정에 있어서 첫번째 할 일은 귀무가설, 대립가설 세우기입니다.

두번째 할일은 유의수준을 결정하는 것이고, 세번째 할일은 귀무가설 및 대립가설을 기각할지 채택할지를 결정하는 것이지요.
세 순서대로 통계적 검정을 진행하죠.

인과관계를 잘 설명해 보이기 위해서는 통계검정보다는 ACF를 이용하는 방법을 추천합니다.

시계열 단위근 존재여부를 판정하는 통계적 검정 방법으로 ADF 검정과 Phillips-Peron 검정이 있습니다.

정상시계열을 판단하는 방법을 실습을 통해 배워보겠습니다.
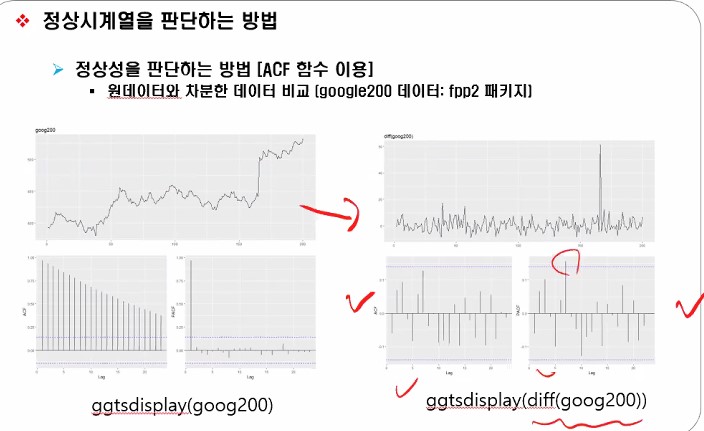
Fpp2 패키지로부터 Goog200(원계열)을 가져와서 goog200을 차분합니다.

실습링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_ACF_PACF.ipynb

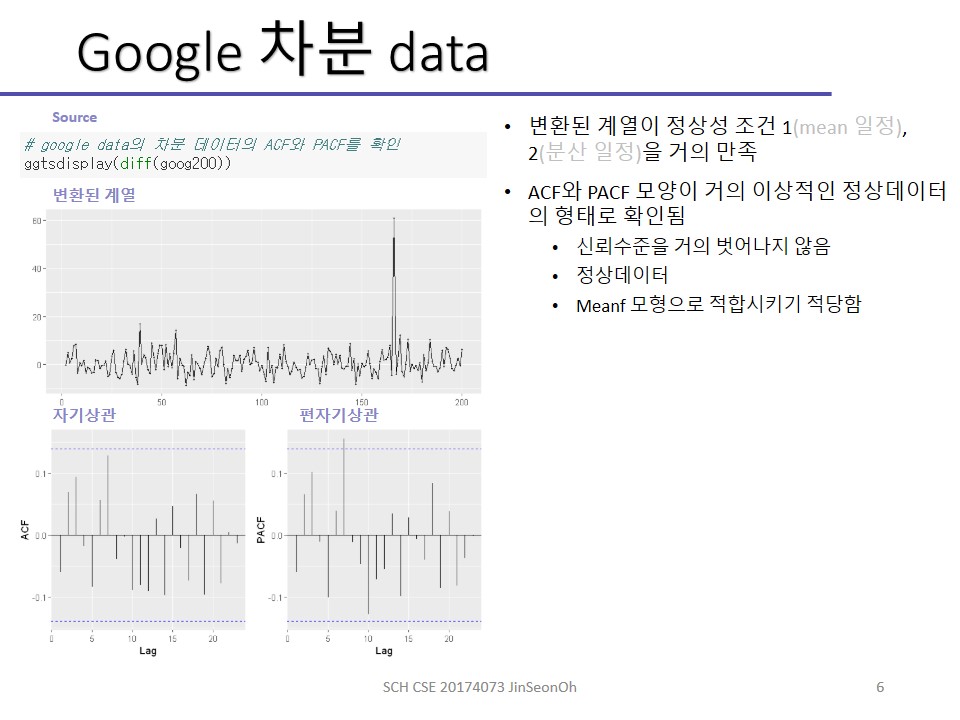
차분 후에는 정상성을 갖는 white noise 형태처럼 보여지는 것을 확인하실 수 있습니다.

체크 표시한경우에는 정상성을 갖으므로 ARIMA로 가심 되구 위에 오른쪽 그림처럼 나오면 meanf를 써야 합니다.

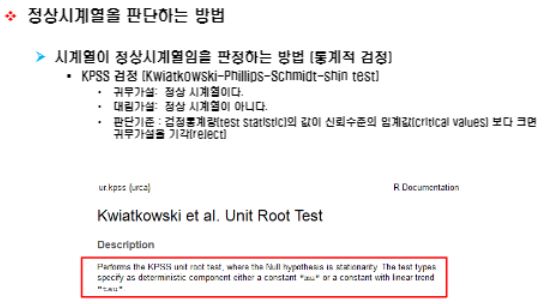
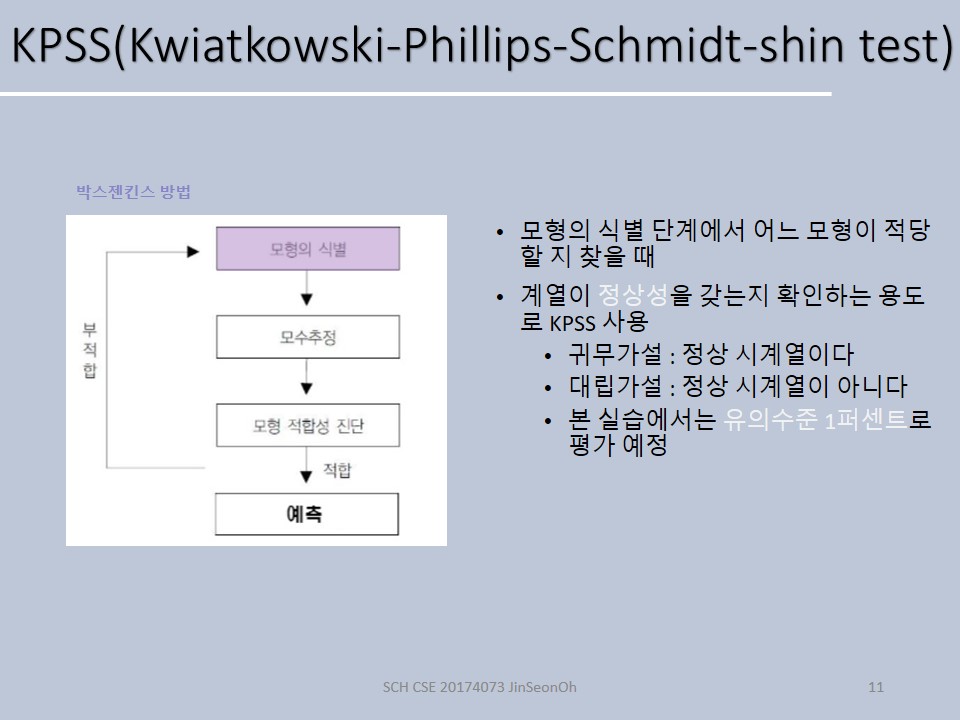
KPSS 검정 KPSS 검정의 귀무가설과 대립가설, 판단기준은 아래와 같습니다.

• 귀무가설: 정상시계열이다.
  
• 대립가설: 정상시계열이아니다.
  
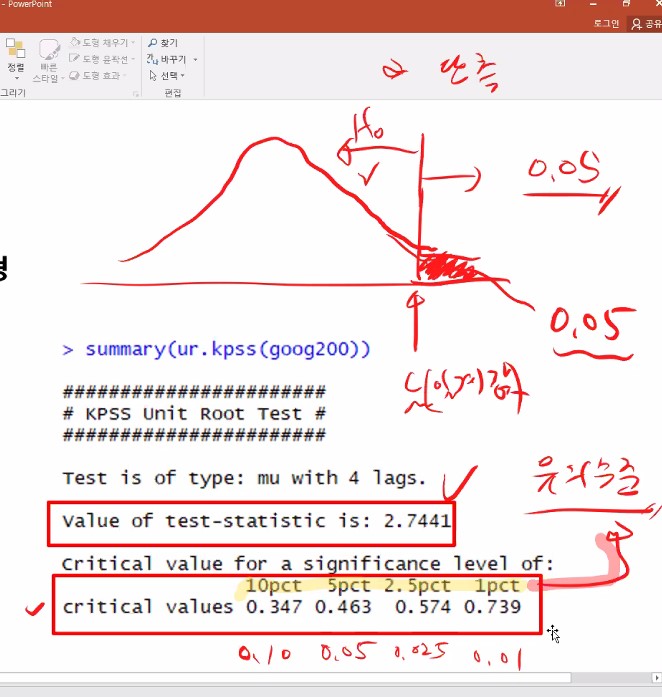
• 판단기준 : 검정통계량(test statistic)의 값이 신뢰수준의 임계값(critical values)보다 크면 귀무가설을 기각합니다.
  유의수준을 정하고 해당 유의수준의 임계값을 보게되는 것 입니다.
  

Null hypothesis가 귀무가설을 말합니다.

귀무가설이란 직접 검증의 대상이 되는 가설로 연구자가 부정하고자 하는 가설입니다.

대립가설이란 귀무가설에 반대되는 사실로 연구자가 주장하고자 하는 가설입니다.

연구자는 귀무가설을 기각하고 대립가설을 채택하고 싶어 하지요.

유의확률과 유의수준에 대한 자세한 설명이 되어있는 링크를 여기에 걸어두겠습니다.

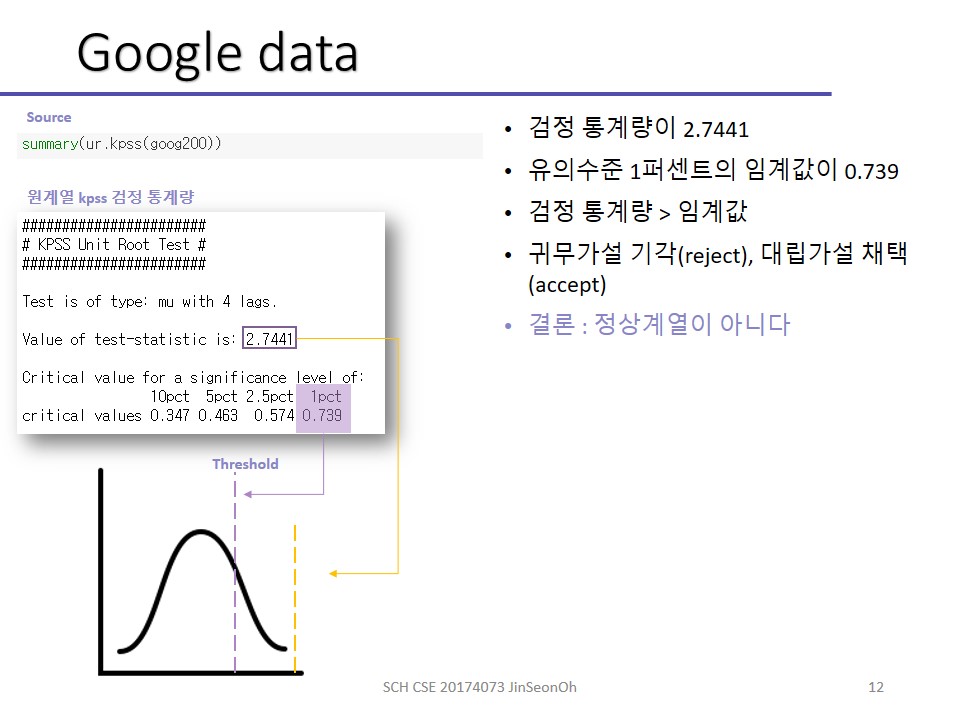
만약 검정 통계량이 2.7441이 나왔는데, 유의수준 1퍼센트가 말하는 임계값이 0.739라면 임계값 이상이므로 귀무가설을 기각(reject)하고 대립가설을 채택하게됩니다.

왼쪽에 있으면 귀무가설H0을 채택해야하고 오른쪽에 있으면 H1을 채택해야합니다.

실습링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_kpss.ipynb

따라서 주어진 구글데이터가 정상시계열이 아니다 라고 이야기할 수 있어지는거지요.

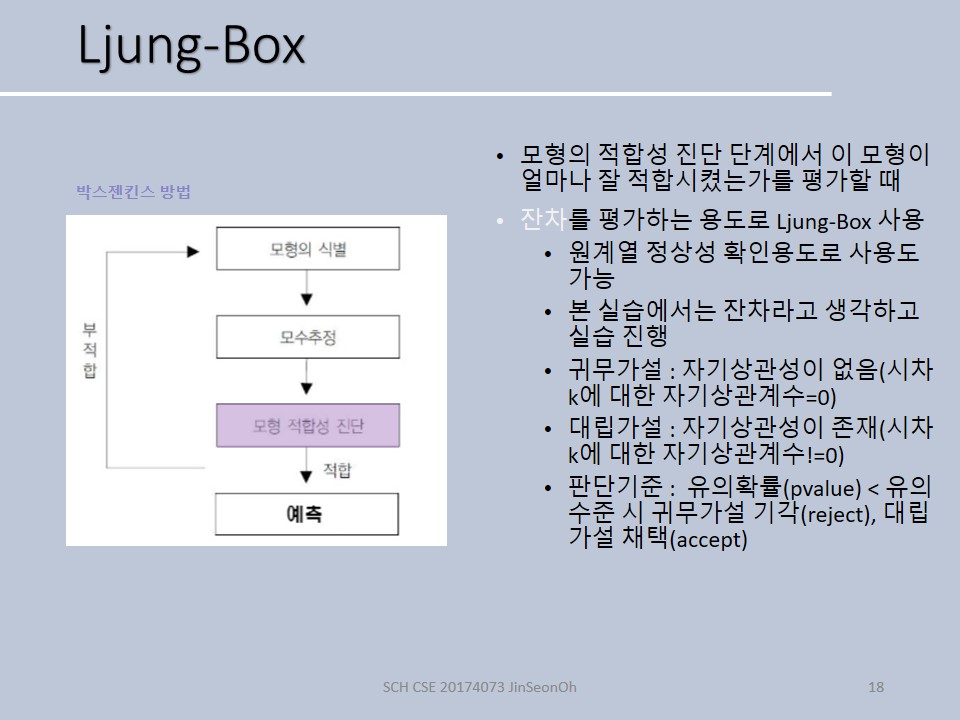
LjungBox 검정 Box piearce 카이제곱 통계량의 수정된 변형인 륭 박스 통계량(portmanteau 검정이라고도 함) 검정은 pvalue로 평가합니다.
실습에서는 원래 데이터가 잔차라고 생각하고 box.test해보았습니다.

륭박스 검정의 귀무가설과 대립가설, 판단기준은 아래와 같습니다.

• 귀무가설: 자기상관성이 없다.
  
• 대립가설: 자기상관성이 있다.
  
• 판단기준 : pvalue가 매우 작으면 귀무가설 기각하게 됩니다. 0.05라는 유의수준으로 잡고 그것보다 pvalue가 작으면 기각하는 것입니다.
  

실습링크: https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_ljungbox.ipynb

1. Kpss 검정으로 하던거 마저 다섯가지 경우에 대해 테스트
   
2. 륭박스로 원본계열을 잔차처럼 이용해서 잔차들끼리 상관성있는지 다섯가지에 대해 확인
   
3. ACF함수 원계열로 ACF, PACF로 ggplot 그려서 평가
   

크게 위 세가지 내용에 대한 실습을 진행한 링크를 아래에 걸어두겠습니다.

• 실습 링크1 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_ACF_PACF.ipynb
  
• 실습 링크2 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_kpss.ipynb
  
• 실습 링크3 : https://github.com/ohjinjin/TimeSeries_Lab/blob/master/lab_ljungbox.ipynb
  

그런데 “잔차”에 자기상관성이 있다는 말은 무슨 뜻일까요??

만약 잔차들이 아래와같이 나왔다고합시다.

ACF 만 봤을 때 lag1234… 시차별로 쭉나오는거거든요?

시차 1일 때 0.9, ….k=n일ㄸㅐ 상관계수값이 0,2… 이런식으로요
잔차에도 이런 패턴들이 나온다는 것은 (시점마다 관계가 있을 것이다)라고 판단을 한다는 것이죠.
시점마다 !!

잔차는 화이트 노이즈 형태로 나와야 잘 나온 것입니다.
시점마다 영향력이 있긴 때문에 저렇게 나왔다고 할 수 있는 거에요

정리하자면

1. 시계열이 정상성을 갖느냐
   
2. 만족하면 ARIMA, ACF, PACF 확인해서 어떤 모형 쓸 건지
   
3. 모형적합시키고 나서 잔차검정
   

1,3번 과정에서 오늘 배운 통계적 방법을 함께 사용해주는 것입니다!

실습에 대한 설명을 이미지로 첨부해놓겠습니다.

개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!