Naive Bayes_Machine Learning(3)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
이번 주제는 학습시간도 테스트시간도 빠르기로 유명한 Naive Bayes에 대한 theory입니다.
과거 이 모델에 대해 스스로 정리한 적이 있었는데 함께 여기에 링크를 걸어두겠습니다.
Naive Bayes
머신러닝에서는 확률을 0~100%로 표현하기보다는 0~1사이로 많이들 표현하곤합니다.
우리는 모든 사건의 확률의 합은 1이 된다는 것을 알고 있습니다.
Naive bayes 모델을 이해하기 위해서는 bayes rule을 선수지식으로 알고 있어야 합니다.
베이즈정리(Bayes Rule)는 아래와 같습니다.
e는 event 또는 evidence, H는 Hypothesis를 말합니다.
P(H|e) = (P(e|H)*P(H))/P(e)
식을 설명하자면, P(e|H)는 Likelihood입니다. 이게 주어진 상태를 가정하지요, 반대로 P(H|e)는 사후확률, Posterior로, 얼마나 이 가설이 그럼직한가에 대한 값입니다.
P(H)는 사전확률, Prior라고 부르며 evidence와는 전혀 상관없이 가설 자체의 확률을 말합니다.
P(e)는 Marginal이라고 부르며, 모든 i에 대해 P(e|Hi)*P(Hi)값의 합을 뜻합니다. 모든 가능한 가설 하에 새로운 사건 e가 일어날 확률인것이죠.
왜 이 정리가 필요할까요?
간단합니다. P(H|e)를 바로 구할 수 없기 때문이죠.
하지만 우변에 있는 모든 값들은 저희가 알아낼 수 있습니다.
문제를 하나 봅시다.
두개의 바구니가 있고, 한쪽에는 빨간공 50개, 파란공 50개가 담겨있으며 한쪽에는 빨간공 30개, 파란공 70개가 담겨있습니다.
- 바구니를 고른다.
- 그 바구니 안에서 공을 꺼낸다.
이렇게 뽑았을 때 그 공이 빨간공이었는데 첫번째 바구니에서 나온 공일 확률을 구해봅시다.
빨간공일 사건을 e로두고 첫번째 바구니일 확률을 H라고 합시다.
그럼 P(H|e)라는 조건부확률을 구해야하는 것이 우리가 해야할 일인데, 바로 구하기 어렵기 때문에 베이지 정리를 이용해서 우회해서 풀어내는 것이죠.
p(e|H) = 첫번째 바구니에서 꺼냈는데 그공이 빨간색일 확률 = 1/2 (첫번째 바구니의 빨간색 비율이 50/100이니까)
P(H) = 첫번째 바구니를 선택할 확률 = 1/2
p(e) = 빨간공일 확률 = p(e|H)p(H) + p(e|H’)p(H’) = 1/21/2 + 3/101/2 = 2/5
혹시 p(e|H)를 (저처럼ㅎㅎ) 1/4라고 구한분이 계시다면.. 너무 자연스럽게 p(e|H)*p(H) 즉, 왼쪽 바구니를 선택하고 동시에 빨간공일확률을 구해버렸던 것입니다.
P(H|e) = (P(e|H)*P(H))/P(e) = (1/2 * 1/2)/(2/5) = 1/4 / 2/5 = 5/8
3/8이 두번쨰 바구니에서 빨간공을 꺼낼 확률입니다.
분모의 marginal을 구하기 위해서는 모든경우를 다봐야해서 computation은 integral할 것을 요구합니다.
그러다보니 분모를 정확한값을 계산하기가 불가능한 경우가 있습니다.
그럴때 Approximation 기법을 이용해줘야하는데 variational bayes, belief propagation 등이 있습니다.
너무 지엽적이니 여기에서는 더 다루지 않습니다.
주요 수식을 다시 한 번 기억합시다.
P(A|B) = P(A,B)/P(B) = (P(B|A)*P(A))/P(B)
Bayes Classifier의 구현은 매우 간단해보입니다.
if P(B\|A)*P(A) > P(B\|A')*P(A'):
x = A사건에 해당
이게 전부죠.
하지만 이것만으로 풀 수 없는 경우가 생깁니다.
예를들어 feature가 두개로 늘어나기만해도 바로 구할수 없어진답니다.
그래서 사용되는 것이 바로 Naive Bayes 입니다.
Naive Bayes Classfier의 구현 시 매우 중요한 Assumption이 있습니다. 바로 Feature들이 서로 독립적이라는 것입니다.
독립적이라면 P(A,B,C)=P(A)P(B)P(C)가 성립하기 때문입니다.
이는 feature간에 상호 커플링 등의 관계가 있다면 성립되지 않습니다.
그래서 P(feature1,feature2|A)P(A) = P(feature1|A)P(feature2|A)P(A)가 성립되어 풀어낼 수 있어집니다.
하지만 여전히 예측확률값이 0이 나올 수도 있다는 risk가 존재합니다. 그래서 normalization을 적용해 이를 해소하기도 합니다.
분포를 이용하는 것이지요.
그 방법론이 바로 Gaussian Naive Bayes 입니다.
지금까지는 P(X|Class)를 단순히 빈도수에만 기반하여 계산했지만, 특정 분포를 따른다고 가정을 할 수 있습니다.
분포에 기반하여 결과값을 얼버무리는 것이죠!
Gaussian Naive Bayes
feature가 독립적이라는 것을 가정하고 naive bayes로 문제를 해결하려했어도 발생했던 문제가 무엇이었냐면, 기존 학습데이터에 한 번도 본적이 없던 데이터가 들어오면 빈도수 기반이었기 때문에 0이라는 값을 얻게되는 문제가 있었습니다.
Gaussian Naive Bayes Classifier를 구현할 때에는 Gaussian 분포를 가정합니다.
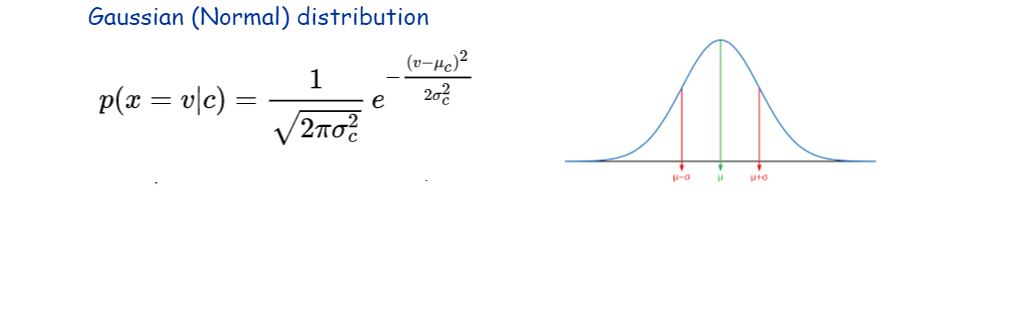
뮤값이랑 스탠다드데리베이션으로 가우시안 모형의 형태를 정할 수 있습니다.
GNB classifier의 학습 과정은 아래와 같습니다.
k번째의 레이블에 대해서 얼마나 그럼직한가에 대해 probability를 분포에 기반해 측정하는데, 그러기 위해서는 모든 feature에 대해 mean값과 스탠다드데리베이션을 미리 계산해둬야합니다.
어떻게 계산할까요? 이걸 설명하기 전에 GNB classifier의 테스트도 확인해봅시다.
새로운 데이터 X에 대해 label Y를 예측하는데, 각 feature에 대해 likelihood를 전부 product(곱)합니다.
P(newX0 | Y=yk) * P(newX1 | Y=yk) * …
이렇게요.
하나라도 0이 나온다면 당연히 결과값도 0이 나올거에요. 이렇게 되면 우리가 앞서 논의했던 Naive Bayes 분류기의 문제점을 만나는 것입니다.
여기까지 구한 값에 레이블 k일 확률(Prior)을 곱해줍니다.
각 레이블마다 이걸 다 구해보고 이 최종 결과값이 최대가 되게 하는 레이블 k를 구하면 됩니다.
여기까지는 본래의 빈도수 기반인 NB 방식입니다.
수식으로 표현하자면 아래와 같습니다.
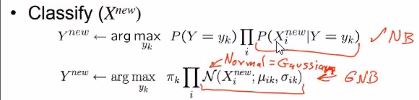
여기에서는 P(Y=yk)는 그대로지만, likelihood들의 곱을 구할때 Normal distribution(즉 Gaussian)을 적용시켜 그 값을 다 곱하도록 하는 것이 바로 GNB입니다.
그저 GNB 모델에서는 likelihood를 구할 때 분포를 기반으로 하는 것 뿐입니다.
참고로 테스트시 y의 label 개수가 N개라고하면, estimate해야하는 P(Y|newX)의 실제 개수는 몇 개만 하면 될까요?
최소 N-1개겠죠! 어차피 확률은 다 더해서 1일테니까요.
그렇다면 학습 때, 정규분포의 파라메터인 mean/variance 값들을 estimate 하는 방법은 뭘까요?
MLE(Maximum Likelihood Estimates)라는 방법을 이용합니다.

소문자 k번째 y라는 것은 k값이 레이블을 구분하는 번호라고 보시면 됩니다.
i번째 x라는 것은 i값이 feature들을 구분하는 번호라고 보시면 됩니다.
i번째 feature랑 k번째 label에 대해 분포가 다 각각 따로따로 존재하는 거에요!
아주 많은 경우가 있겠죠.
k에 대한 feature i에 대한 평균(뮤)을 구하는 과정은 아래와 같습니다.
참고로 모종의 함수δ는 j번째 레이블이 k번째 레이블과 같으면 1, 그렇지 않으면 0을 반환하게됩니다.
1/(k 레이블을 가진 데이터들의 개수)*(모든 k레이블 데이터 중에서 i라는 feature들만의 값을 모두 더한 값)
즉 말 그대로 평균값을 구한 것입니다.
표준편차를 구할때도 마찬가지로 수식을 이해하면됩니다.
각각의 레이블과 feature에 대해 구한 mean값으로부터 + | - 얼마나 떨어져있는지 그 거리만을 나타내기 위해 제곱해서 이용하면 되겠습니다.
학습시 이렇게 파라미터들을 각각 다 구하게 될겁니다.
그래서 각 feature에 대해서만 따로 스탠다드 데리베이션을 주는 방법도 있고, i번째 feature에 독립적으로 각 레이블마다 스탠다드데리베이션을 주는 방법도 있습니다. 아예 둘다 빼버리고 모든 feature와 label에 대해 단 하나의 스탠다드데리베이션을 적용시키는 방법도 있습니다.
이런 vairance를 가정하게되면 파라미터 수가 매우 줄어들겠죠!
어쨌든 이렇게 학습되어진 GNB의 decision boundary의 모양은 어떨까요?
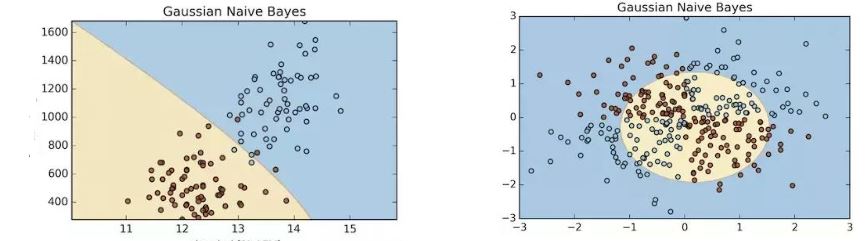
probability distribution 모양에 따라 boundary 모양이 바뀌는 것을 볼 수 있습니다.
하지만 XOR과 같이 비선형 패턴의 문제를 해결할 때도 잘 찾아낼 수 있을까요? 그렇지 못합니다.
왜냐하면 가우스 분포모형(probability distribution )을 3차원으로 사상시켜보면 그렇게 생겼기 때문이에요.
타원에 동그라미하나 있는 생김새입니다. 학습에 실패하면서 그 모양을 끝까지 따라간 것 입니다.
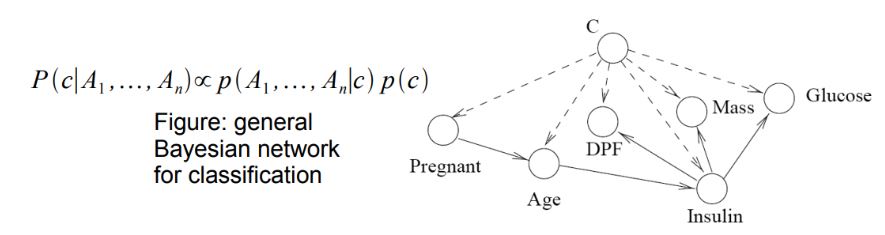
Bayesian Networks
Bayesian Network는 랜덤 변수의 집합과 방향성 비순환 그래프를 통하여 그 집합을 조건부 독립으로 표현하는 확률의 그래픽 모델입니다.
베이지안 네트워크의 한 가지 이점은 복잡한 결합 분포(complete joint distribution)보다 직접적인 의존성(a sparse set of direct dependecies)과 지역 분포(local distribution)를 사람이 이해하는데 직관적이라는 것입니다.
[출처:https://ko.wikipedia.org/wiki/%EB%82%98%EC%9D%B4%EB%B8%8C_%EB%B2%A0%EC%9D%B4%EC%A6%88%EB%B6%84%EB%A5%98](https://ko.wikipedia.org/wiki/%EB%82%98%EC%9D%B4%EB%B8%8C%EB%B2%A0%EC%9D%B4%EC%A6%88_%EB%B6%84%EB%A5%98)
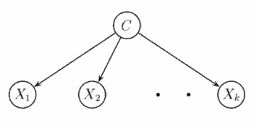
Bayesian Network로 NB를 표현할 수도 있으며 보다 general한 모델이라고 볼 수 있겠습니다.
Bayesian Network를 보다 쉽게 설명하자면, “내 짐작에 저 데이터는 이런 방식으로 생겨 났을 꺼야” 라는 가정을 통해 접근을 해 모델을 학습 시켜 가장 잘 부합되는 네트워크를 찾는 것입니다.
무엇인지 자세히 알아봅시다.
feature A와 feature B로부터 영향을 받은 feature C를 수식으로 표현하면 아래와 같습니다.
p(A,B,C) = p(C|A,B)p(A)p(B)
그리고 그림으로 표현하면 서로 독립된 A노드와 B노드가 C노드를 가리키는 모양입니다.
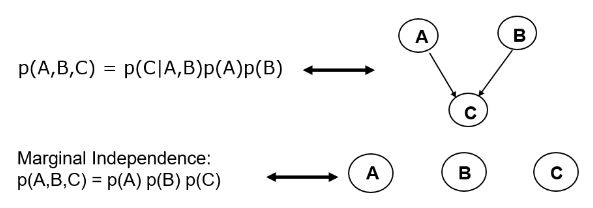
이런 것을 Bayesian Network, Belief network, Causal network라고도 부릅니다.
다시 정리하자면 방향이 있는 간선의 경우 direct dependence를 뜻하고, 간선이 없다면 조건부독립을 뜻합니다.
베이지안 네트워크를 이해하기위해서는 6가지 기본 규칙을 먼저 알아야합니다.
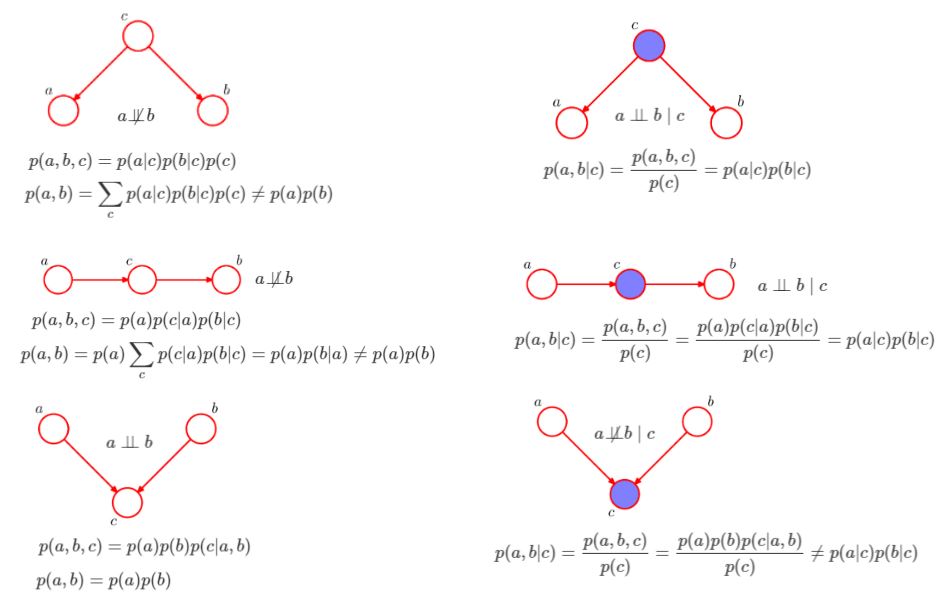
왼쪽부터 상단부터 오른쪽 하단 순서대로 1~6번이라 칭하겠습니다.
또 이 그래프를 볼때 참고로 아셔야할 것이 있는데 색칠이 된 것은 값이 주어졌다는 뜻 입니다!
1번 규칙에서 보면 c가 주어져있지 않기 때문에 c에 대한 marginalizing out으로 a와 b가 독립이 아니다라는 것을 말합니다.
(cf) 마지널라이징 아웃=c가 안정해진 상황을 고려하는 것)
2번 규칙은 c가 정해졌다면 a와 b는 상호독립이라는 것을 말합니다.
3번 규칙은 a에 의해 c가 결정되며, c에 의해 b가 결정이 되므로 b값을 좌우하기때문에 a와 b가 독립이 아니라고 말합니다.
4번 규칙은 c값이 일단 정해지면 a와 b는 독립이라고 설명합니다.
5번 규칙은 상호 독립이던 a와 b가 c에 대한 결정에 영향은 주겠지만 말 그대로 a와 b는 독립이라고 말하며,
6번 규칙은 c가 결정이 되었을 경우로, explaining away에 의해서 독립이 아니라고 설명합니다. explaining away는 c의 값에 대한 당위성을 설명하기 위해 서로 연관없는 a와 b가 애쓰는 상황을 말합니다.
저는 여기까지 배웠을 때 그게 궁금하더라고요,
예를 들어 4번 규칙같이 연쇄된 네트워크에서 c가 주어지면 a와 b가 독립이다 라고 설명하는데, 근데 c는 a에 의해 영향을 받는 feature일텐데 a보다 먼저 결정이 되었다라는게 뭔가 인과적으로 어색해보여서 와닿질 않더군요.
저처럼 궁금하신 분들이 계시다면 저는 아래 내용으로 답변을 보고 해소가 되었어서 ㅎㅎ 공유해드립니다.
Bayesian network 는 나의 hypothesis 에 기반해서 ‘설계’한 것일 뿐입니다.
실제 관측되는 데이터에서는 어떤 노드가 관측되는지는 상황에 따라 달라질 수 있습니다.
그에 따라서 우리가 풀어야 할 문제도 달라질겁니다.
가령, a -> c -> b 라고 설계를 했어도, c 가 주어진 상황에서 a와 b 를 예측하는 문제를 풀수도 있어지는 것이지요.
Baysesian Network는 앞에 주어진 현상 또는 지식, 가설을 기반으로 generative하게 설계를 하는거에요.
많은 문제를 풀수 있어요 당연히 classificaition 문제도 풀 수 있습니다.
각각의 feature들의 관계를 edge로 표현을 하고 call해가며 각각의 확률을 보는거죠.
아래 그림은 클래스 C에 대한 관측을 그린 것 입니다.
Posterior는 likelihood에 prior를 곱한것과 비례한다고 말하고 있습니다.
NB분류기를 구현할때는 label로부터 각 observation이 영향받는다는 가정하에, 각 feature(observation)들이 서로 독립적이라고 가정하에 그려줍니다.
베이지안네트워크는 굉장히 자유도가 높은 네트워크입니다.
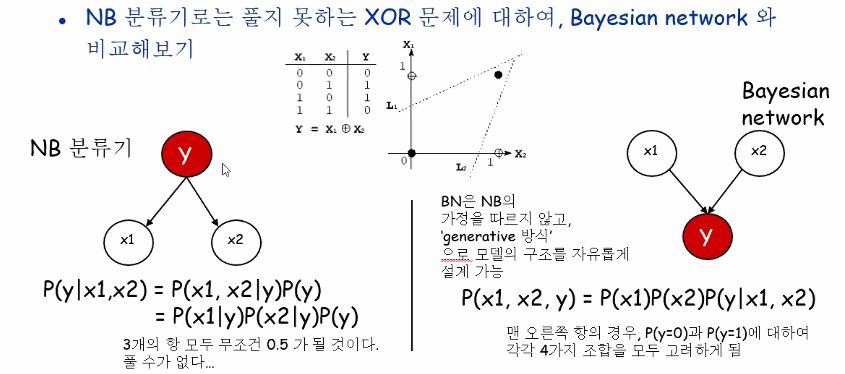
사실 NB로는 풀 수 없는 문제가 있어요, 앞에서 잠시 봤었는데 바로 XOR 문제였죠.
각각의 0,1 x값들이 feature들이 되며, Y 값이 즉 label이 class라고 보시면됩니다.
NB로 이 문제를 해결하려고하면 결정장애를 겪게 될 겁니다 ㅎㅎ.
P(x1, x2, y) = P(x1)P(x2)P(y|x1,x2) 이 BN수식을 이렇게도 쓸수 있을까요?
P(x1, x2, y) = P(x1)P(x2)P(y|x1)P(y|x2)
x1의 2가지 경우, x2의 2가지경우 총 네 가지경우로 모 나눠서 볼 게 아니라 두 가지경우로만 볼 수 있을까하는 문제인데, 하지만 위 그림에 주어진 예제의 경우에는 불가능합니다.
왜냐하면 P(x1,x2|y) != P(x1|y)P(x2|y)이기 때문이죠.
우리가 배웠던 규칙 6번에 의해서 y값이 주어져있으면 x1과 x2 feature는 각각 독립이 아니기 때문에 저 수식이 성립하지 않는 것입니다.
explaining away 상황이 발생하기 때문이라고 배웠지요!
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!