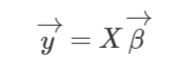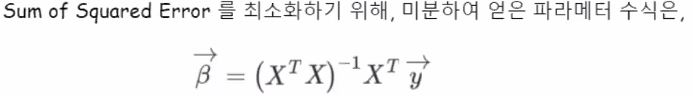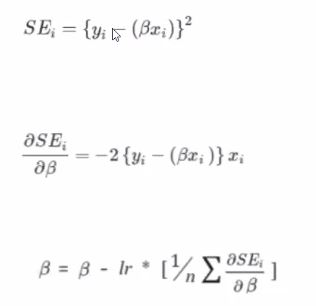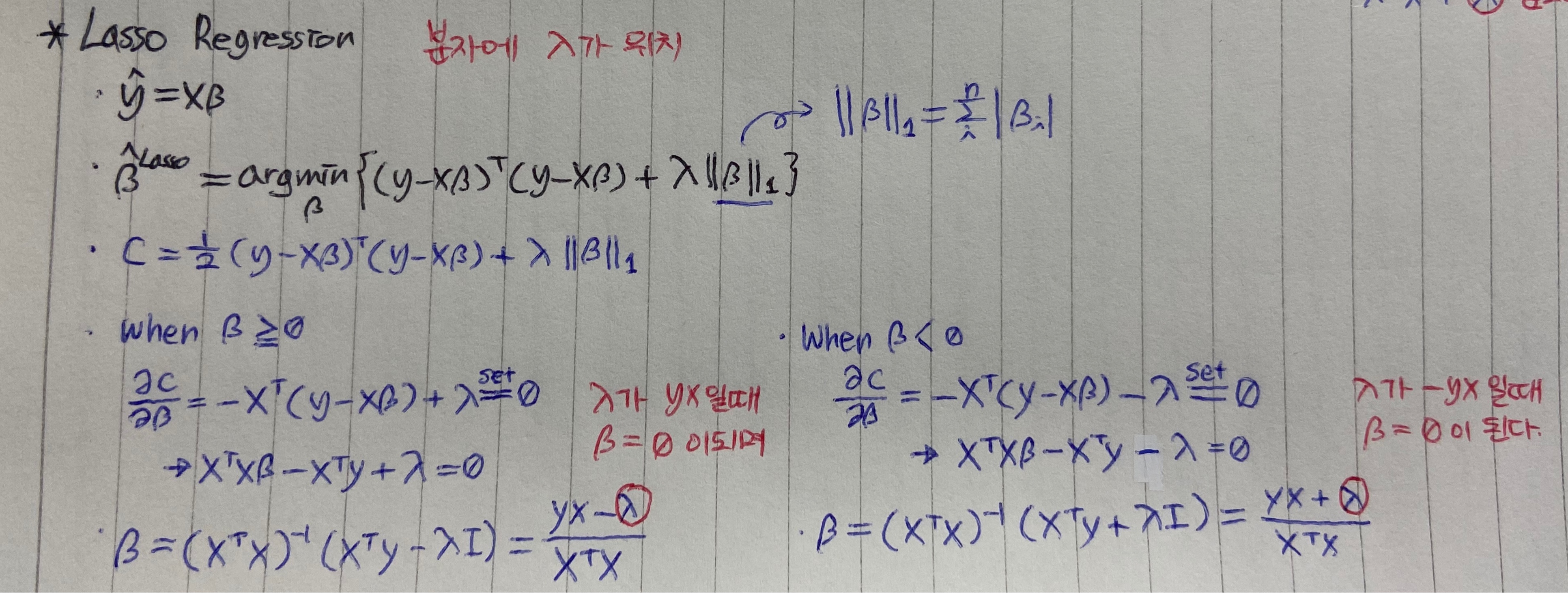Linear Regression_Machine Learning(4)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
이번 주제는 Linear Regression에 대한 theory입니다.
Linear Regression
여태 우리가 배웠던 모델들은 classificaion이었습니다.
하지만 이번엔 regression 모델을 배울 겁니다.
둘의 차이를 간결하게 설명하자면 classification의 예측 결과값은 클래스 또는 레이블입니다.
그리고 regression의 예측 결과값은 실수입니다.
이 동물이 고양이일까 개일까 가 아니고, 내일의 주가가 얼마일까? 예측하는 느낌입니다 ㅎㅎ
linear 모델은 아래와 같이 표현됩니다.
X가 feature vector, 베타는 파라메터들, y는 예측값입니다.
파라메터가 뭘지 와닿지 않으신다면 선형방정식 y=ax+b에서 a와 b를 묶어놓은게 베타에 해당하는 것입니다.
데이터를 가장 잘 설명하는 베타 값(기울기, 절편)을 갖는 직선을 찾는 것입니다.
그래서 특정 x값을 갖는 새로운 데이터가 들어왔을 때 우리가 미리 구해놓은 직선의 방정식에 의해 그의 y값을 찾는 것이 바로 linear regression입니다.
최적화 하는 부분에 있어서 위수식만으로 계산이 안되기 때문에 대안으로 사용하는 iterative한 방법으로 학습을 하는 방법도 있습니다.
예제를 보겠습니다.
- 데이터
(2,5) (3,7) (4,9) (5,11)
선형모델은 ax + by + c =0이라고 가정합니다.
여기서 a, b, c가 위에서 말한 베타인데, a=1,b=1,c=-5로 초기값을 가정합시다.(초기값 설정에 대한 연구도 활발합니다)
그러면 우리의 hypothesis는 x+y-5=0입니다.
-
데이터 대입
학습과정은 위 데이터를 hypothesis에 대입하는 것부터 시작됩니다.
y값이 3,2,1,0이 나왔겠죠? 정답은 5,7,9,11인데 말이죠. -
오차함수값 계산
Loss = (y-y’)^2, Cost = Mean-Squared-Error라고 하면, total loss와 total cost는 아래와 같습니다.- total loss = (5-3)^2+(7-2)^2+(9-1)^2+(11-0)^2=214
- total cost = 214/4=53.5
- total loss = (5-3)^2+(7-2)^2+(9-1)^2+(11-0)^2=214
당연히 loss와 cost는 낮아야 좋겠죠? 그래서 우리는 cost를 최소화시키는 방향으로 파라메터를 갱신해줘야 합니다.
- 갱신
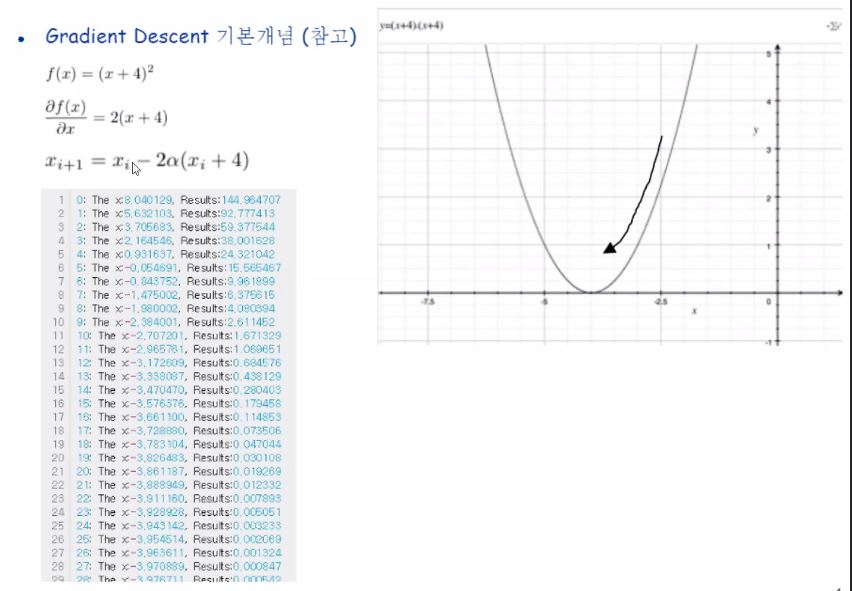
Gradient Descent를 적용하여, MSE가 가장 작은 a,b,c를 찾아갑니다.
gradient는 우리가 고등학교 때 배웠던 미분입니다.
오차함수값이 최소가 되는 지점으로 갱신하기 위해서 기울기의 개념을 차용하여 최소로 내려가는 방법입니다.
더 자세히 설명해보겠습니다.
현재 시점에서 해당하는 오차함수값이 있을겁니다.
오차함수값이 그 값일때의 기울기를 계산하고 그 기울기의 반대 방향으로 가며 갱신하는 것입니다.
왜냐하면 양의 기울기일때는 왼쪽으로 가야(음의 방향으로 가야) 최저점에 도달할 수 있으며, 반대로 음의 기울기일때는 오른쪽으로 가야(양의 방향으로 가야) 최저점에 도달할 수 있기 때문이지요.
위 그림에서의 세번째 수식에 있는 알파값은 학습률이라고 부르며 갱신하는 보폭의 크기를 말합니다!
너무 크면 최저점에 수렴은 커녕 발산해버릴 수 있으며, 너무 작으면 학습이 너무 오래, 한참 걸리게 될 것 입니다.(오버피팅의 우려도 존재)
참고사항: Cost 함수가 convex 모양이어야 최소값(최적위치)을 찾을 수 있습니다.
그렇지 않다면 Global 최소값을 구하기 어렵겠지요. 보장도 되지 않을 꺼고요.
이 개념을 저희가 지금 배우고 있는 Linear Regression 에 적용해봅시다!
참고로 SE는 Squared Error를 말합니다.
다시 한 번 정리해보자면 오차값을 최소로 하는 베타값을 찾는 것이 학습과정인 겁니다.
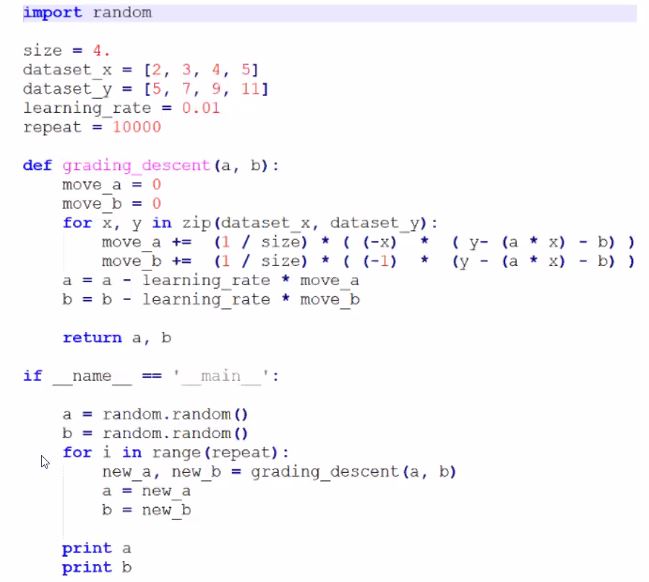
linear regression에 대한 예제 소스코드를 분석해봅시다.
이 소스코드에서는 학습 완료시점을 오차값이 0이 되는 지점까지가 아니고 10000번의 회수를 정해주었네요.
그리고 파라미터들의 초기값 설정은 랜덤으로 했다는 것을 알 수 있습니다.
Ridge, Lasso Regression
linear regression의 파라메터들이 너무 커지는 것을 방지하기 위해 나온 모델입니다.
무슨 말이냐하면 우리는 y=2x+3은 2y=4x+6과 동치인걸 알고 있습니다.
각 계수값들이 우리가 학습시키는 파라메터라고 했었잖아요? 그 계수들이 너무 커지지 않게 막으려는 거에요 왜 커지면 안되냐하면.. overfitting 될 수 있기 때문이에요.
(cf) 왜 파라메터가 크면 오버피팅이 되는 지 찾아보았는데 저처럼 궁금하실 수 있는 분들을 위해 예를 공유해드립니다.
주어진 데이터에는 항상 이상적인 데이터만 있는 것이아니고 어쩌다 한 번씩은 튄 값이 있을텐데 이때 방정식의 계수가 너무 크다면 영향이 넘 크게 오니까 전반적으로 그런 현상을 완화시킬 목적으로 사용되는 것이 패널티와 L2 정규화 개념입니다!)
또한 Ridge regression은 오버피팅 방지 말고도 다중공선성을 방지하는 목적으로도 사용된다고 합니다.
궁금하신 분들 께선 잘 설명된 포스팅 공유해드립니다!
https://m.blog.naver.com/PostView.nhn?blogId=vnf3751&logNo=220833952857&proxyReferer=https:%2F%2Fwww.google.com%2F
Ridge regression은 L2 norm으로써 파라메터가 커지는 것을 제한합니다.
아래 이미지에서 ridge regression의 마지막 항이 그에 해당하며 이것 때문에 제한이 생기는 것 입니다!
linear regression의 식을 보면 오차 제곱을 최소화 시켜주는 아규먼트 베타를 찾아주겠다는 뜻입니다.
rigde regression 식을 보면 오차는 그대로 있고 람다에 베타 제곱을 곱한 항도 더해주잖아요?
이건 쉽게 설명하자면 베타의 값도 최소화시켜주려고하는 겁니다!
참고로 람다가 클수록 제한이 강해집니다.
이렇게 제한을 두는 과정을 정규화라고도 합니다!
lasso regression도 비슷합니다. L1 norm으로써 제한하는 모델입니다.
베타의 크기(절대값)만을 고려해준뒤 람다를 곱한 항을 더해주는데, 마찬가지로 그 최종값이 최소가 되도록하는 베타를 구합니다.
근데, 절대값함수는 미분이 안되므로 미분이 아닌 다른 여러기법을 적용해서 최적화시켜줘야하는 이슈가 있다는 것을 기억해주세요.
또한 Ridge에 비해서 Lasso가 더 타이트하게 감소시켜줍니다.
그 이유는 왜 일까요?
위에 잠시 말한 것 처럼 Lasso는 regularization term이 절대값이므로, 절댓값함수는 첨점이 존재하는 함수로서 미분불가합니다.
반짤라서 0보다 크거나같을때, 0보다 작을때로 각각 나누어 gradient를 구해 그 값을 최소화시키는 베타를 찾는데 그 과정에서, 즉, ‘베타’에 대한 최적값 수식을 전개해보면 ‘람다’가 분자 부분에 위치하게 됩니다.

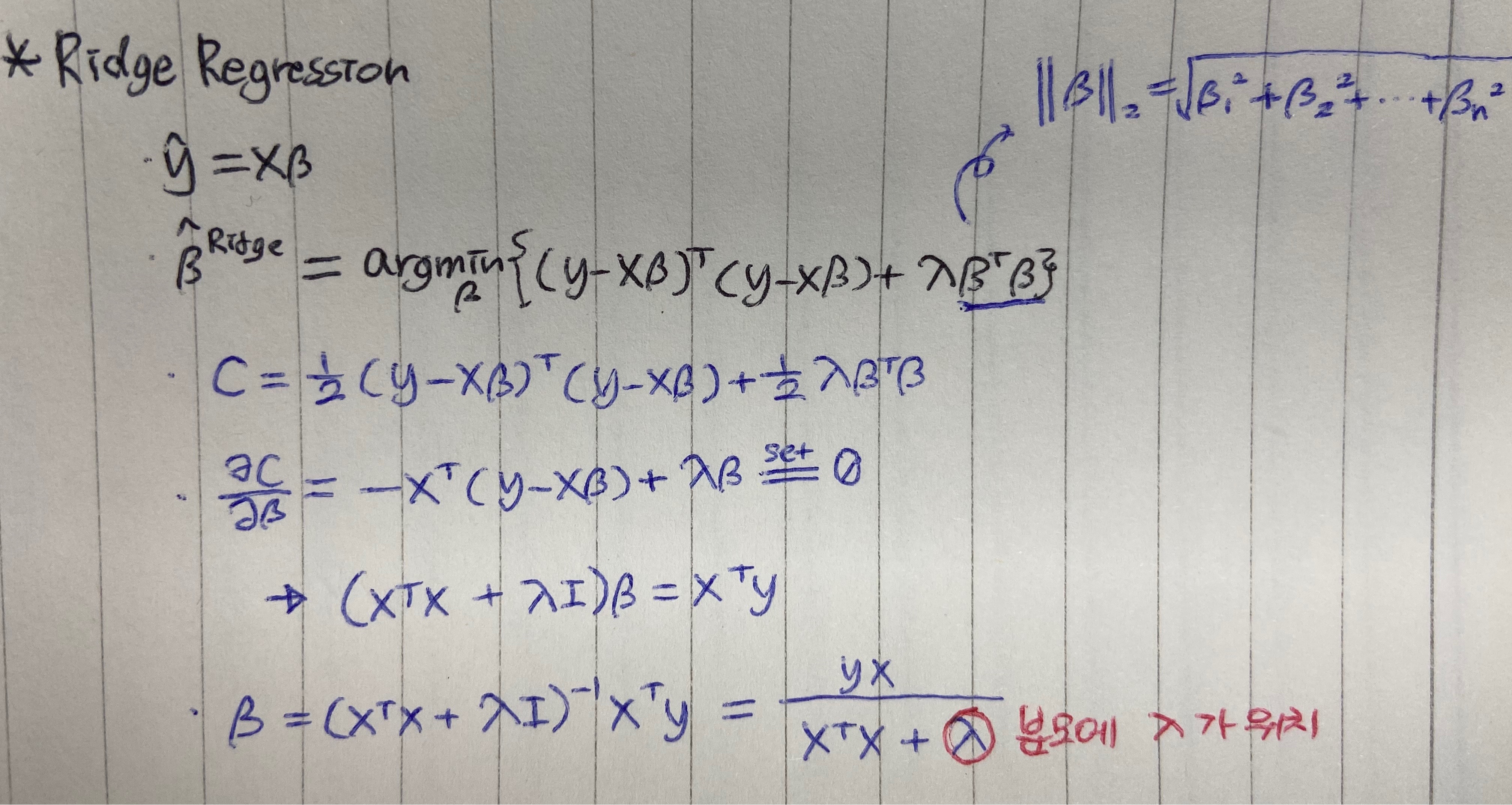
이는 그라디언트 하강법 식 전개시 람다가 분모에 위치하여 아주 미미한 feature 하나하나를 학습 끝까지 결국 놓지 못하고 여지를 남겨두는 ridge regression와는 다릅니다.
분자에 람다값이 위치한다는 것은 ‘람다’의 값에 의해 ‘베타’값이 0이 될 수 있는 가능성이 열리게 된다는 말이며, 쉽게 말하면 신경안써도 되는 애들(0이 된 애들)을 걸러버릴 수 있다는 효과를 가진다는 말이 됩니다.
우리는 그 특징을 바로 feature selection이라고 부릅니다.
그래서 더 제한이 강하다고 말할 수 있는 것입니다.
보통의 경우 신경쓸부분에만 신경쓰니까 베타 최적화에 더 유리해져 linear, ridge보단 성능이 높게 나오지만, 단점으로는 크게 보면 필요했을 수 있는 정보를 손실할 위험이 있어 또다른 대안책들이 있기도 합니다.
Linear Classification
logistic regression을 이용한 linear classification을 봅시다.
저희는 여태까지 XB와 같은 선형합을 구하는 방법으로 regression을 배웠습니다.
그런데 이러한 함수를 채용하여 classification에도 적용을 시킬 수 있답니다.
기존의 회귀문제를 맞출때 그 답은 label이 아니라 어떤 real number가 결과로 나왔었지만, classification 문제에 적용하기 위해서는 선형합에 대한 임의의 함수를 적용하여 확률값을 생성해줄 필요가 있습니다.
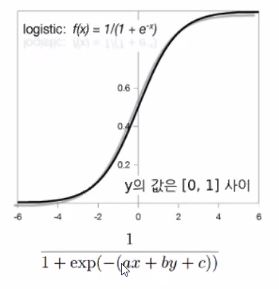
확률값을 생성해주는 함수가 바로 logistic function입니다.
이 함수의 인자 범위는 -무한대~ +무한대까지이며, 함수값의 범위는 0~1사이의 값을 갖게됩니다.
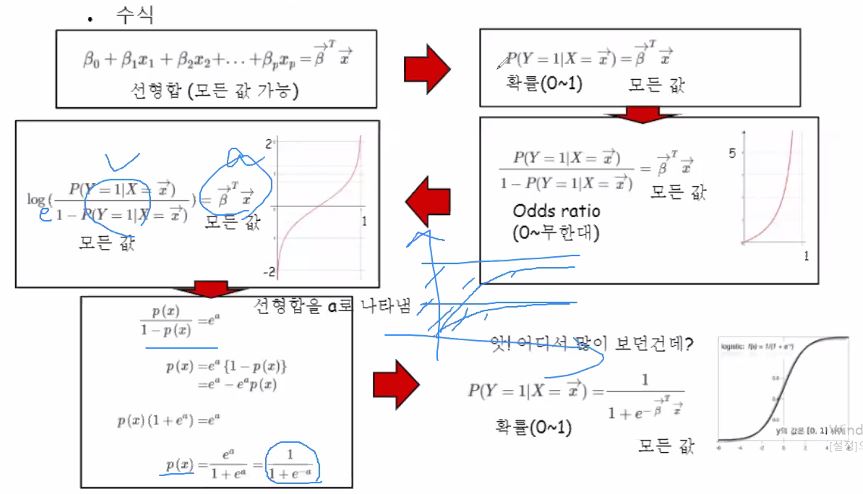
그럼 logistic function이 만들어진 motivation을 살펴볼까요?
로그함수는 모노토닉 함수중 대표적인 함수입니다.
odds ratio에 로그까지 씌우면 -무한대 ~ +무한대 까지의 모든 값을 생성해 낼 수 있습니다.
설명이 잘 되어있어 위 사진대로 이해해주시면 될 것 같습니다!
확률값을 구하도록 logistic funcion을 이용하지 않더라도 꼼수로 classifier를 구현할 수는 있습니다.
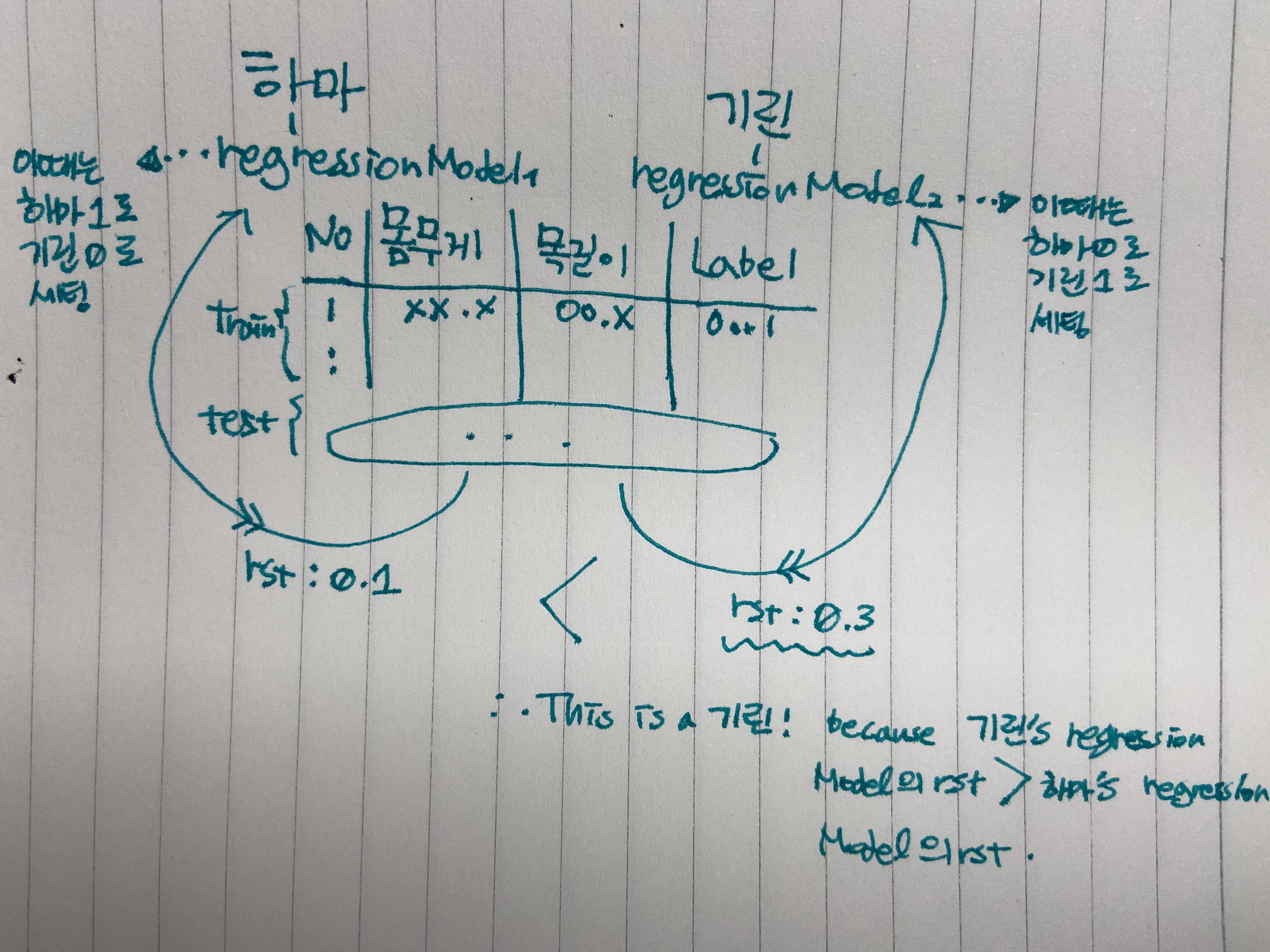
바로 multi response linear regression이라는 방법인데요, 각 클래스별로 Regression 모델을 적용해 대소비교를 함으로써 구해내는 방법입니다.
아래에 참고자료를 첨부해드리도록 하겠습니다.
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!