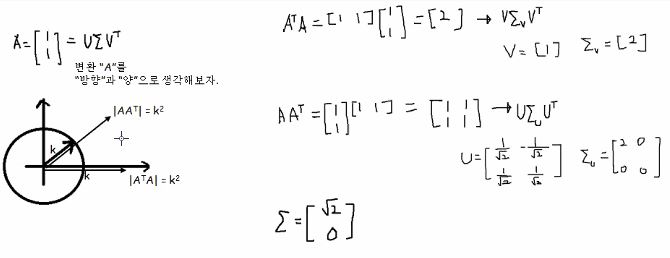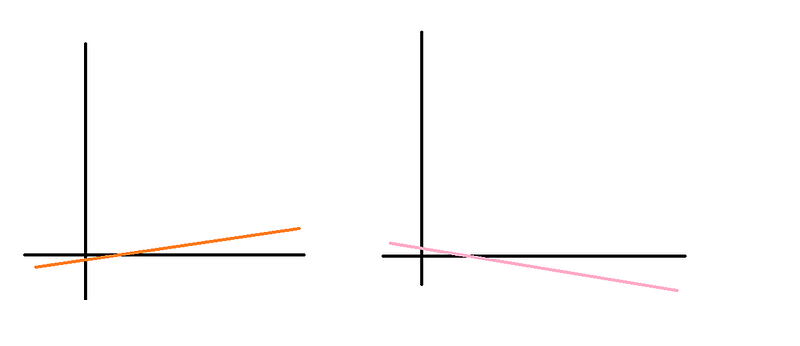SVD & PCA & LDA_Machine Learning(6)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
이번 주제는 SVD에 대한 theory입니다.
SVD에 대해 배우기 전에 선수 지식으로 Linear Algebra의 기반 지식들을 정리하고 갑니다.
Linear Algebra 배경지식
- 기저, 좌표계
임의의 벡터집합 S에 속하는 것들이 서로 1차 독립이면서 어떤 벡터공간 V를 생성하면, S를 V의 기저라고 합니다.
좌표계가 생성되지요.
우리가 흔히 알고있는 2차원 좌표계의 기저는 x축과 y축이되며, 3차원 좌표계의 기저는 x,y,z축이됩니다.
- 고유값, 고유벡터
행렬 A에 대해서 Ax = 람다 x를 만족할때 람다는 고유값(scalar), x는 고유벡터입니다.
참고로 1xn이나 nx1 행렬은 열벡터 또는 행벡터라고 부를수 있게되어서 그러한 행렬은 벡터라고 혼용해서 칭합니다.
우리는 고유값과 고유벡터를 사용함으로써 해당 기저의 고유공간에서 확대/축소, 회전 등의 변환을 할 수 있습니다.
벡터v에 대해 어떤 transformation을 적용해서 나온 결과 벡터 v를 람다v라고 표현하고 있네요.
예제를 들어 먼저 한번 설명해보겠습니다.
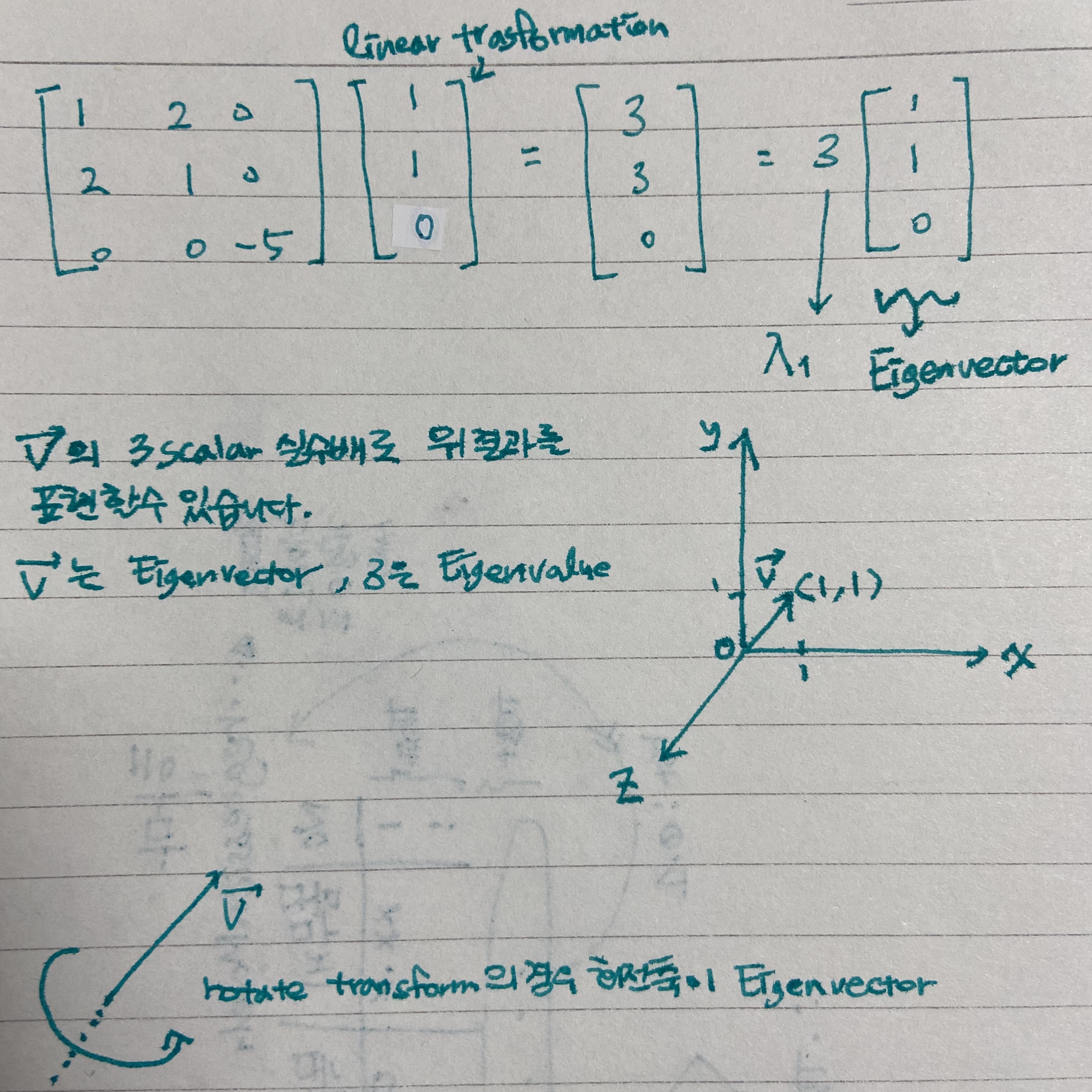
아래 그림처럼 결과행렬은 고유값과 고유벡터로 표현해낼 수 있는 것입니다.
[1 1 0]은 우리가 구하는 첫번째 고유벡터, 3은 우리가 구하는 첫번째 고유값이 됩니다.
원행렬에 A 변환을 적용했을때 어떤 결과벡터가 나오는데, 도대체 그 결과는 어떤방향으로(고유벡터) 몇배늘리거나 줄이거나 했길래(고유값) 나오게 된 것일까?라고 보시면됩니다.
v1과 v2를 기저로 갖는 공간에서 고유값1 고유값2 배만큼 변환이 적용된 것이지요.
고유벡터를 어떻게 구하는 방법이 궁금하실 겁니다.
어떠한 선형변환을 가하는 연산자 역할을 하는 것이 위 식에서 A 입니다.
고유벡터는 A 행렬을 곱함으로써 변환을 가하더라도 그 결과가 자기 자신 고유벡터로서 다시금 표현이 가능해야합니다.
그말인 즉슨, 변환 전의 벡터와 A를 적용해서 변환을 가한 후의 벡터가 서로 평행한 관계라는 조건을 갖는 것이 고유벡터가 가질 조건이라는 뜻 입니다.
평행하기 위한 조건은 또 무엇일까요? [1 1]과 [3 3]은 평행합니다.
[1 1]과 [-3 -3] 역시 평행합니다. 역방향 벡터더라도 몇배의 실수배를 하던지 간에 절대 접점이 없다면 평행하다 말할 수 있습니다.
이러한 조건을 만족하는 특수한 벡터가 바로 고유벡터인데, 일반적으로 임의의 정방행렬 nXn인 A 행렬에 대한 고유벡터는 n개입니다.
보통 A의 고유벡터를 구할 때는 A에 A의 전치행렬을 곱하고 특성방정식으로 람다(고유값)를 구하고, 그에 대응하는 고유벡터를 구하게 됩니다.
자세한 예제가 잘 나와있는 블로그 포스팅 링크를 여기에 걸어드리겠습니다.
그래서 아래의 또 다른 예제를 보시게되면요,
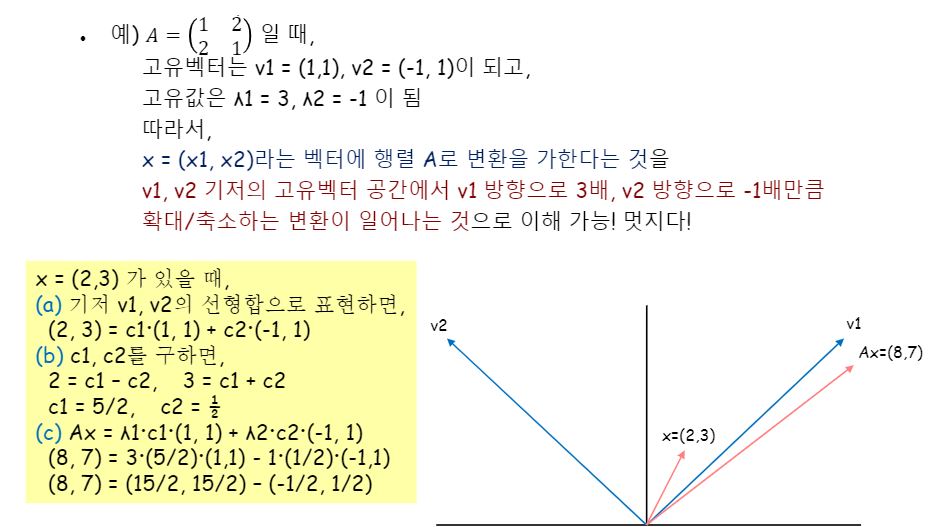
2x2 정방행렬 연산자인 A에 의해 고유벡터가 v1, v2 두개 나온 것을 확인하실 수 있습니다.
A*v1은 어떤실수배*v1으로 표현이가능하며, 이때 어떤실수배는 3이라는 스칼라값이 됩니다!
A*v2 역시 -1이라는 스칼라값으로 변환 전인 v2벡터로 표현이 가능합니다.
바로 이러한 스칼라값이 고유값입니다.
고유벡터(EigenVector)와 고유값(EigenValue)는 우리가 곧 배울 SVD, EVD, PCA, spectral clustering, Eigenface 등 많은 곳에서 응용될 것이기 때문에 기초적으로 알고 계셔야합니다.
- Rank
- Column Rank : 선형독립인 열 벡터의 최대개수
- Row Rank : 선형독립인 행 벡터의 최대개수
행렬의 Rank를 구하기 위해서는 행사다리꼴로 정의한 이후에야 비로소 한눈에 보실 수 있습니다.
- Column Rank : 선형독립인 열 벡터의 최대개수
EigenValue Decomposition
고유값 분해를 배워봅시다.
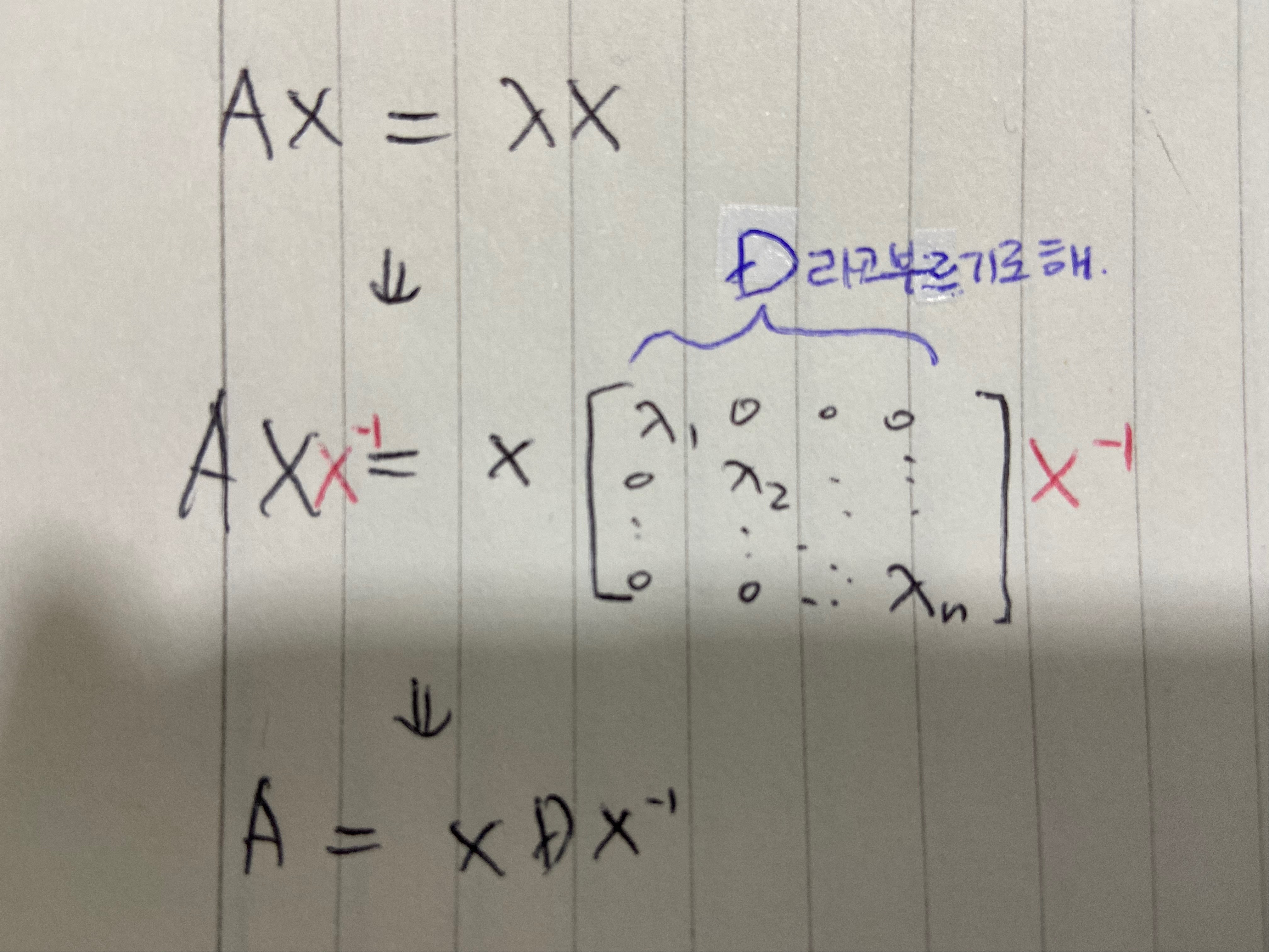
NxN 크기의 정방행렬 A에 대하여, 3개의 행렬(및 벡터)의 내적(PDP를 말함)으로 나타낼 수 있습니다.
AX=람다x라는 식과 A=PDP의역행렬라는 식은 똑같은 말을 하는 식입니다.
그 이유는 아래 그림에 나타내었습니다.
아래 그림에서 X를 P라고 이해하시면 편합니다.
다시 한 번 변환하는 단계를 이해해봅시다.
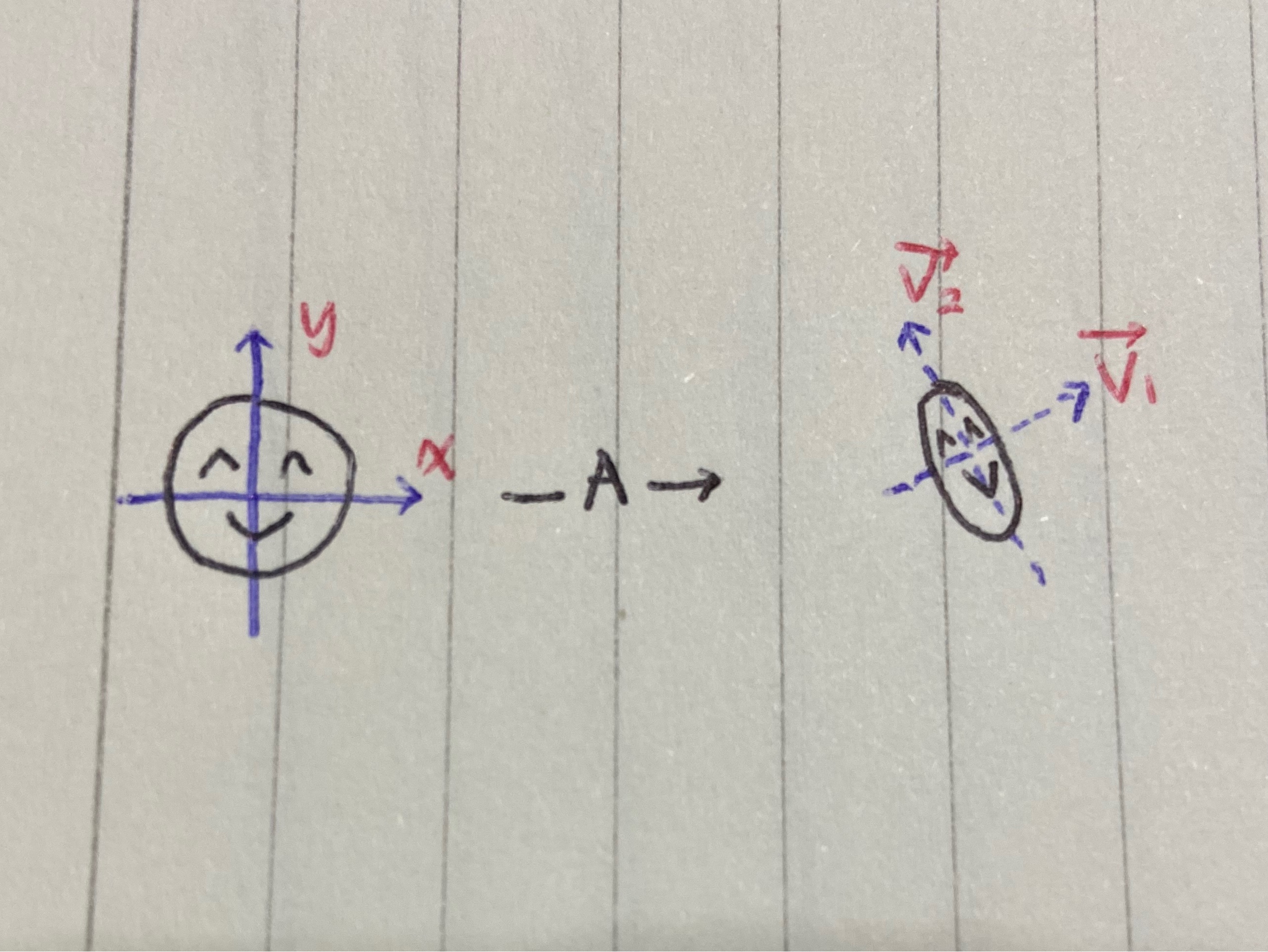
고개를 돌려서 찾아야겠죠!
SVD(Singular Value Decomposition)
다시 고유벡터와 고유값을 살펴보면, 정방행렬일 때로 가정하여 설명한다는 것을 알 수 있습니다.
그렇다면 정방행렬이 아닌데 분해할 수 없을까?에 대한 일반화된 분해법이 SVD(Singular Value Decomposition)입니다.
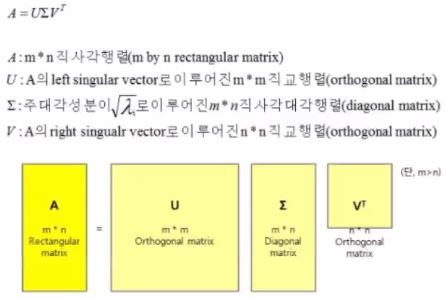
MxN 행렬 A(변환해주는 연산자 역할)에 대해 3개의 행렬 내적으로 나타낼 수 있습니다.
시그마는 일부만 대각성분이 람다로 채워져있고 나머진 0으로만 이루어진 행또는 열을 가지게 되는 행렬입니다.
SVD의 개념을 이해해봅시다.
어떤 임의의 차원의 값을 새로운 차원으로 바꿀 수 있는 거에요!!
단 컴파스 그린 것 처럼 같은 양의 것으로만 바꾸는 거지요.
원래 있던 차원을 없애고 새로운 차원이 생겼다고 받아들여봅시다.
eigenvalue decomposition에서는 A를 바로 분해했는데, SVD는 다른 애를 이용해서 정방행렬로 바꿔준 다음에 eigenvalue decomposition해주게 됩니다.

참고로 고유값 구하는 방법은 아래 특성방정식을 풀어 람다에 대해 정리해 풀어낼 수 있습니다.




이것이 아까 말한 차원을 높였다해도 양은 그대로 라는 말입니다.
2차원 공간 상에서의 양과 4차원 공간 상의 양이 같은것이죠.
다시 SVD를 정리해봅시다.
Eigenvalue Decomposition을 적용하기 위해 mxn 직사각 행렬을 정사각행렬을 만들때 A^tA를 통해서 그리고 AA^t를 통해서 분해해줘야해요.
전자(A^tA)는 nxn으로, 후자(AA^t)는 mxm으로 변환해준것이라고 보시면 됩니다.
전자는 낮은차원으로의 변환을 2번한거고, 후자는 높은차원으로의 변환을 2번한겁니다.
전자는 U에 해당하고 후자는 V에 해당하는 겁니다.
이제 가운데 X부분만 설명이 남았는데요, 왜 람다를 쓰긴쓰는데 굳이 루트를 씌울까요?
첫번째 디컴포지션과 두번째 디컴포지션의 양은 일치했다는 것을 우리가 알게 되었었죠.
근데 곱하잖아요? 행렬말고 실수 개념으로 비유해 보자면 마치 k*k=k^2이니 원래값을 확인하기 위해 루트를 씌워주는거라고 보시면 편합니다!
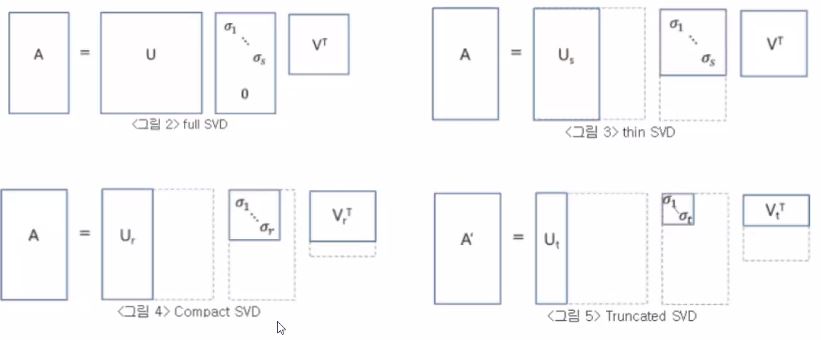
지금까지 설명한 것들을 그림과 함께 다시 정리해봅시다!
SVD의 종류는 방금 배운 FullSVD 보다는 축약된 버전인 reduced SVD가 많이 활용됩니다.
작은값에 대한 값만 남게 된다고 보시면 됩니다.
저기 다시 정리해보기로 했던 2x1짜리 A에 대한 SVD 예제에서도 보면 람다가 한개밖에 없다는거 확인 되시죠? 1차원이든(A^tA) 2차원이든(AA^t)지요!
설사 다른 직사각행렬이 더 길다해도 작은애에 맞춰버리겠단거에요!
애초에 mxn이라는 디멘젼 정보를 가지고 있기때문에 이게 가능한 겁니다.
그래서 첫번째 reduced SVD인 thin svd는 0인 성분들 다 무시하는 것이며, 두번째 reduced SVD인 compact svd는 계산하고 보니 rank가 부족했던 경우가 있을 수 있어서 그런 추가적으로 확인된 0 성분들을 마저 빼고 계산한 다음에 마지막에는 0이었기 때문에 뺐던 것들을 추가만 하면되는 것입니다.
결과는 똑같을 거라는 전제를 두고서요.
세번째 reduced SVD인 truncated svd는 원본행렬 A의 랭크가 r이었는데 그보다도 더 작은 개수 t만큼 줄여버리는겁니다.
그냥 0이 아니어도 우선 날려버리는거죠. 메모리는 많이 절약되겠죠?
그렇지만 원래 0이 아니었는데도 없앴으니 이전의 값은 알 수 가 없겠죠? 다시 원래 차원대로 맞추기위해 0이었다고 가정하고 마지막에 메꿔넣어줍니다. 엥?! 싶으시지 않나요?
그럼 완전히 다른값이 나오는데 이걸 왜? 어따 써먹지? 싶으실거에요!
일부러 해상도를 떨어뜨리려고 하는 등 압축을 목적으로 사용한답니다.
하지만 만약 끄트머리 성분들이 만약 핵심적이었다면 치명적일 겁니다.
그렇지만 열중에 아홉 이상의 경우 좌상단에 있는 애들이 주성분이기 때문에 저희가 잘라내는 아래쪽의 성분들은 없애더라도 크게 문제가 되지 않습니다.
우하단에 위치할수록 그림의 디테일을 표현하는 애들이 나오게 됩니다.
만약 제 얼굴이 있는 원본 사진이 있었는데, truncated svd로 압축을 시켰다고 가정합시다.
truncated svd를 적용함으로써 아래쪽 성분 조금 없앴다해도 “(해상도가 낮긴한데) 이건 오진선의 얼굴 사진이군!” 하고 알아볼 수 있습니다.
심지어 조금 과하게 없애도 “누군가의 얼굴을 찍은 사진같군!”라고 판단할 수 있을 수준일거에요.
그런데 만약 왼쪽 위 부분의 성분을 없앤다면? “이게 무슨 사진이지?”가 될 수 있어요!
PCA(Principal Component Analysis)
한국어로는 주성분 분석이라고 합니다.
데이터의 분포에 대한 주성분을 찾는 것입니다.
여태 공부했던것처럼 핵심 ‘축’을 찾는 것으로부터 가능해집니다.
조금 더 고급지게 표현하자면, 데이터의 패턴을 잘 표현해주는 최적의 feature, 또는 성분만의 조합을 찾는 것입니다.
그래서 PCA는 featur selection 혹은 feature dimension reduction을 위해 사용되곤 합니다.
어느 feature가 효율적일지 골라낼 능력이 있기 때문이지요!
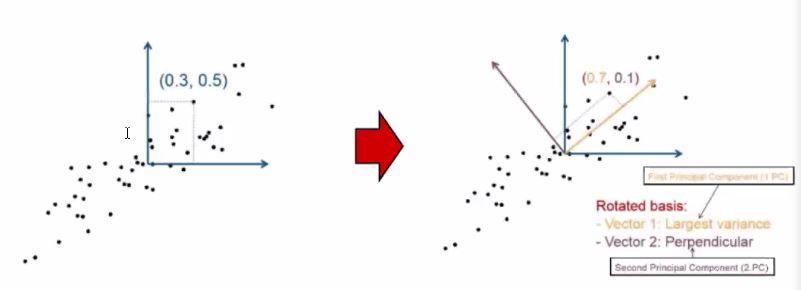
PCA 구하는 방법을 살펴봅시다.
- 데이터들의 평균(중심)으로 원점을 가정
- 데이터들에 대한 공분산행렬, 고유값, 고유벡터 구함
- 고유벡터 기반(관점=축=여기선 pca를 말함)으로 데이터를 보면, 가장 큰 분산을 가지게 됨
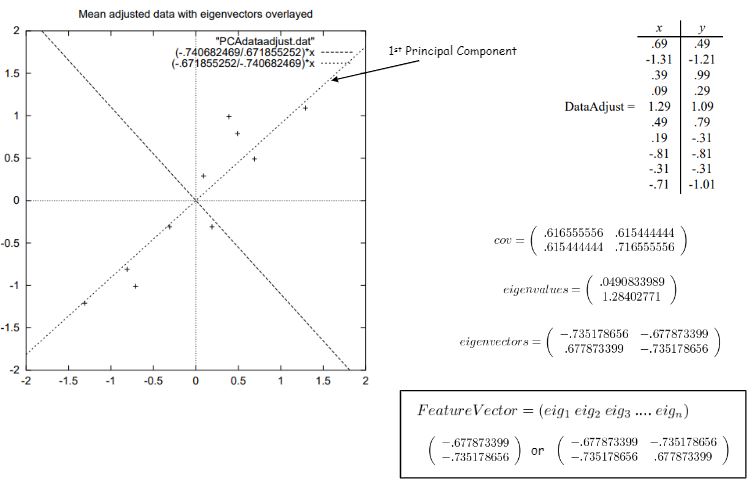
공분산(covariance)이란 무엇일까요?
얼마나 너희 성분들끼리 동시에 늘거나 줄어드니? 에 대한 것을 수치화 시킨게 공분산입니다.
서로 다른 feature들의 값에서 각각 mean을 빼면 그거는 분산이잖아요?
(위 그림에 나와있는 수식 중 y에 바를 씌운게 mean값이에요.)
그래서 공분산은 두 변량이 각 평균으로부터 변화하는 방향 및 양에 대한 기대값이 됩니다.
feature가 m개있으면 각 pair를 보기 위해 mxm의 행렬로 나오는게 공분산행렬입니다.
즉, 서로 연관이 있는 feature pair들을 파악할 수 있게 됩니다.
feature pair는 다른말로 correlation이라고 합니다.
이에 대한 고유값과 고유벡터를 얻는 것은 결국 correlation이 존재하는 feature들에 대해 기저를 확보하는 작업이라고 이해할 수 있습니다.
고유벡터를 기저라고 가정하고 데이터를 보게 되면, correlation이 컸던 feature pair들의 관점(축)으로 보게 되므로 당연하게 분산이 커지는 것 입니다.
핵심은 원점 옮기기와 공분산행렬 구하기, 그리고 그 행렬을 이용해 eigenvalue와 eigenvector를 구하는 것입니다.
당연히 공분산행렬이 mxm정방행렬이니까 고유벡터는 m개로 나오겠죠?
PCA 스텝은 아래 순서로 이루어집니다.
- data Matrix X가 주어졌을 때 모든 데이터 샘플에 대한 평균을 구합니다.
- 각 데이터 샘플에서 구했던 평균을 뺀 값들에 대한 매트릭스 D를 정의합니다.
- 1/(N-1)DD^T 즉 D와 D의 전치행렬의 곱에 1/(N-1) 스칼라를 곱한 covariance Matrix, 시그마를 구합니다.
- 시그마에 대한 고유값과 고유벡터를 계산합니다.
- 해당하는 고유값을 기준으로 고유벡터를 정렬합니다.
- 가장 큰 고유값을 갖는 고유벡터를 선택합니다. 선택된 고유벡터 W는 PCA projection space를 나타냅니다.
- D를 PCA 아래의 차원공간에 사영시킵니다.
예시를 봅시다.
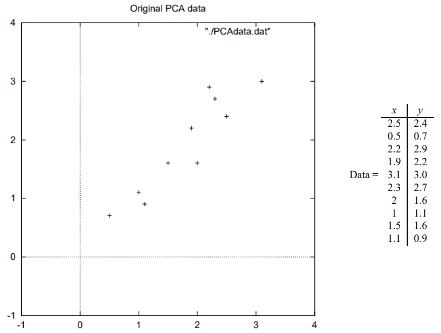
첫번째꺼가 두번째꺼보다 낫잖아요?
예제에서는 한놈만 PCA로 가정하겠어! 하고 1번 축을 선택합니다.
그 고른 pc를 원 데이터(feature vector)에 곱해줍니다.
그다음은 고른축으로 각 feature vector들을 사영 시킵니다.(수선의발을 내립니다.)
그 결과 성분들을 다 구하면 됩니다.
PCA의 주된 활용도는 압축이며, 분산이 작은 것을 중요하게 여기는 데이터/어플리케이션에는 적합하지 않고, 데이터들의 분산이 직교하지 않는 경우에도 적합하지 않습니다.
위 예제의 경우에는 2차원이다 보니 사람의 직관으로도 PCA를 찾는 것이 가능하지만, feature dimension이 큰 경우에는 어렵겠지요.
PCA와 유관한 알고리즘으로 Independent Component Analysis 라는 것이 있습니다만 커리에서 이에대한 설명은 생략합니다.
LDA(Liner Discriminant Analysis)
머신러닝하는 사람들 사이에서 LDA라고 하면 목적이 전혀 다른 유명한 알고리즘이 있어서 혼선이 있을 수 있으니까 주의해주세요. ㅎㅎ
한국말로는 선형판별분석이라하며, fisher라는 사람이 만들어서 fisher’s algoritm이라고 부르는 사람들도 있습니다.
PCA가 Feature selection에쓰인다고 이야기를 했습니다.
우리가 배웠던 eigen value랑 eigen vector로부터 계속 파생해서 배우고 있었어요.
예제를 먼저 봅시다.
여기서부터는 클래스!라는 말을 씁니다.
클래스 두개가 있다고 가정을하고 판별을합니다.
원본에서의 우리의 feature dimension은 x,y축이라고 합시다.
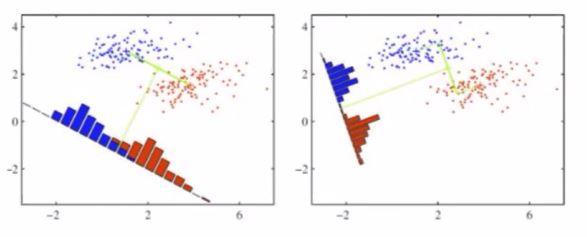
특정 관점에서 두 클래스가 겹쳐보인다면 좋은 관점이라 할 수 없습니다.
가로축을 기준으로 데이터를 본다 하면 파란 클래스와 빨간 클래스 사이에 겹치는 구간이 생기잖아요? 그럼 잘 나누질 못한 거겠지요?
그럼 반대로 세로축 기준으로 보면 어떤가요? 그렇다해도 겹치는 구간이생기지요. 깔끔하게 나뉘질 못합니다.
가로축 디멘젼과 세로축 디멘젼이 기본으로 주어져있고 이들 축을 기준으로 구분해보자니 잘 되질 않으니 새로운 feature dimension을 찾자는 데에서 착안합니다.
앞서 배웠던 PCA가 뭐였나요? 데이터를잘 나타내는 feature dimension을 찾는 것 이었잖아요? 그벡터에 기반하여 데이터들이 포진이 되어있으면 좋은 예 였구요.
새로운 축을 찾는 것이라는 점에서는 PCA와 LDA가 비슷해 보일 수 있습니다.
PCA는 잘 나타낼 선을 찾는 것이 목적이었다면, LDA는 구분할 선을 찾는 것이 목적이 됩니다.
큰 차이는 두 가지에서 나오게 됩니다.
그 두 차이를 보기 전에 앞서서 위 예제에서 오른쪽 그래프를 한 번 확인해봅시다.
겹치는 구간이 거의 없이 잘 나누고 있지요?
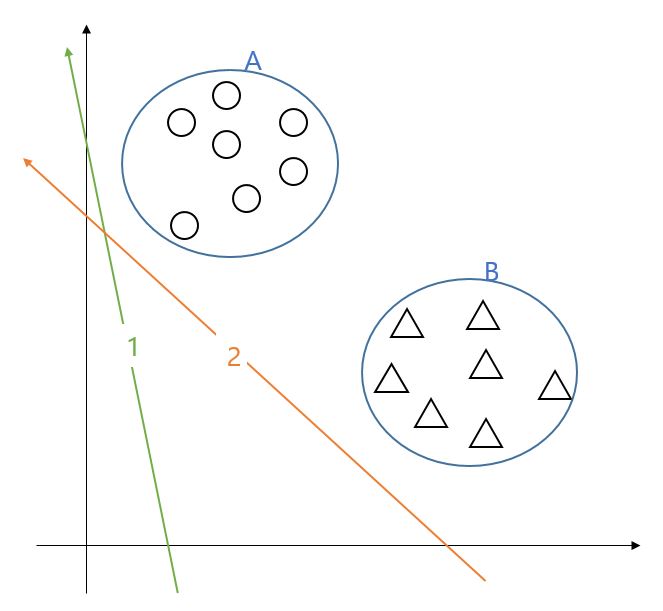
예제를 하나 더 봅시다.
1번 벡터와 2번 벡터둘 다 잘 나눈 것처럼 보이시나요?
그럼 어느 벡터가 더 잘 나눈 것일까요?
이렇게 생각해봅시다. ML 모델을 생성할 때에는 학습용 데이터와 테스트용데이터로 나누기로 했잖아요?
테스트 데이터가 어디에 있을지 알 수가 없는 것이거든요.
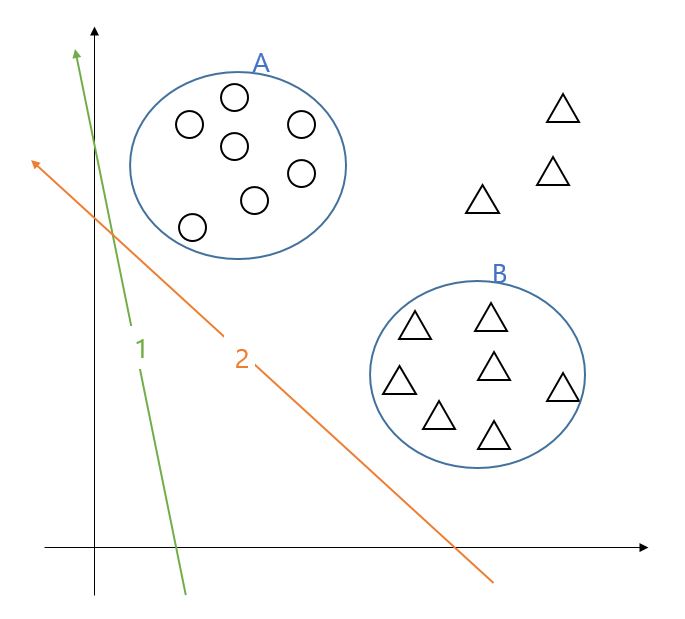
1번 축도 2번 축도 두클래스를 잘 나눌 수 있어 보이지만, 테스트 데이터는 제가 파란색선으로 그린 원 밖으로 벗어날 수도있겠죠?
아래 그림처럼요.
이럴 경우엔 1번보다 2번벡터가 더 잘 뽑힌거잖아요?
성능 테스트는 위와 같은 상황을 당연히 포함하기 때문에 모델은 그런 점까지 고려해줘야 할 필요가 있습니다.
고로 클래스 A 중심과 B 중심사이를 최대화시키는 벡터가 좋은 벡터가 됩니다.
쉽게 말해 혹시 모를 상황을 위해 거리가 멀수록 좋다는 이야기랍니다.
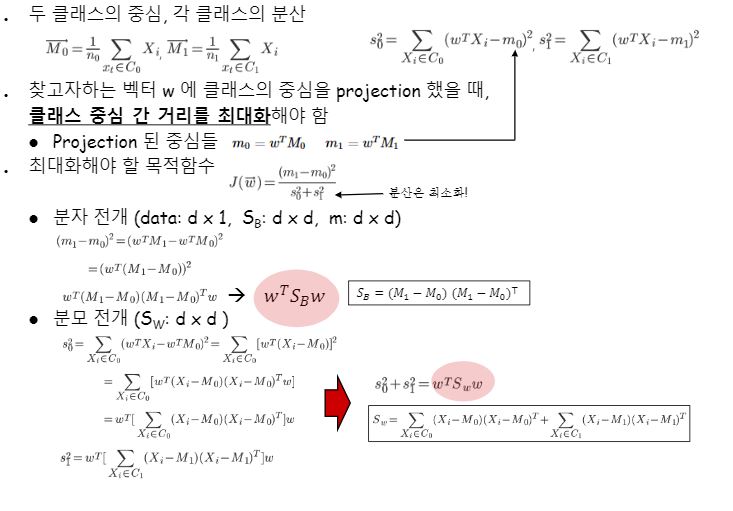
수식을 알아봅시다.
두 개의 클래스 C0, C1가 있다고 가정합니다.
원래 주어졌던 두 기저(쉽게 말하면 x,y)에 기반하여 n개의 데이터가 존재한다고 합시다. (x1,y1), (x2,y2), … , (xn,yn) 이렇게요.
이들 데이터들은 하나하나가 x성분과 y성분을 갖는 벡터에요.
(2차원이니까)이들의 중심이 되는 좌표가 있겠죠? 그 중심점 역시 x성분과y성분을 갖는 하나의 벡터로서 표현될 것입니다.
예를 들어 (2,1), (4,3), (6,5)라는 세 데이터의 중심은x성분에 대한 (2+4+6)/3과 y성분에 대한 (1+3+5)/3 값으로 (4,3)이라는 중심점이 나오는 것처럼요.
이렇게 클래스별로 중심을 구한 후 클래스의 데이터들을 전부 사영해서 분산들의 합을 구합니다.
중심점 벡터를 구할때는 기존 기저인 x,y 성분들로 하지만 w축에 대해서 보는거니까 그 값을 그대로 쓰기엔 적절하지 않을 수 있어서 w축에 사영시켜서 값을 이용하게 되는 것이라고 이해했습니다.
이 과정은 다시 말하면 중심을 기준으로 얼마나 뭉쳐있는가 하는 응집 정도를 보는 것입니다.
참고로 클래스별 분산의 합을 구할 때는 저희가 구하는 w축에 사영(project)시켜서 w축을 기준으로 얼마나 떨어져있는지만 보고 높이는따지지 않습니다!
예제에서는 중심점 벡터를 사영시킨 스칼라값을 m0와 m1이라고 각각 부르고 있습니다.
이 목적함수가 이야기하는 것이 무엇이냐?하면 클래스 중심간 거리는(=분자) 크게 하고 클래스의 데이터간 응집도는(=분모) 높았으면 좋겠다 라는 것입니다.
왜냐하면 클래스끼리 잘 뭉쳐져 있어야 당연히 구분이 더 쉬우니까요!
위 캡처에서는 각각 SB랑 SW로치환하여 정의해서 간단히 표시하고 있습니다.
그리하여 목적함수를 간략화시키구요, 이 목적함수를 최대화하기 위해 편미분을 해주는 것이지요. 다른 말로는두 클래스간 거리는 크게하면서 각 클래스별 응집력(중심점으로부터 얼마나 해당클래스 데이터들이 떨어져있는가)은 작게하는 w축을 찾기 위해 편미분을 해주는 거라고할 수 있습니다.
최대화 시키는 w를 구하기 위해 편미분값을 0으로두는 것을 확인하실 수 있을 겁니다.
왜 0으로 둘까요?
이건 미적분학에 대한 지식입니다.
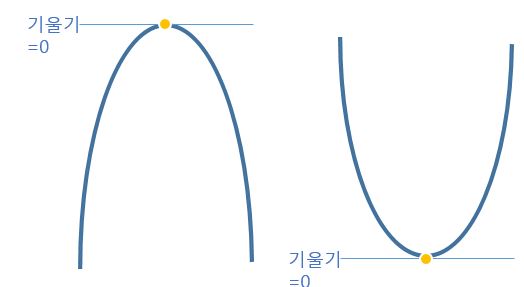
우리가 “어떤 이차함수 값이 최소 또는 최대가 되게 하는 x값을찾는다”는 말을 편하게 “최솟값 또는 최댓값을 구한다”고 표현하곤 하는데요.
그 때 그 어떤 이차함수의 도함수 값이 즉 기울기가 0이되는 지점의 x값을 최소 또는 최대값이 되게 하는 x값이라고배웠잖아요? 그래서 0으로 두는 거에요!
어쨌든 편미분값=0으로 두고 방정식을 풀어나가다보면 위 캡처이미지처럼w값을 찾을 수 있게 되는데요, 그렇게 찾게 된 축에 threshold를 두어 더 작으면 클래스 A, 더 크면 클래스 B로 구분 짓도록 classifier를 구현합니다.
그런데 만약 비선형으로 분포되어있다면 혹은 응집되지 않은 분포를 가지는 데이터를 만난다면 이 모델은 적절하지않을 수 있습니다.
LDA를 PCA와 비교해봅시다.
PCA는 클래스를 구분 짓지 않고 그들을 잘 나타내는 축을 찾는 것이며, LDA는 구분 지을 축을 찾아 분류기에 적용할 수 있다는 차이가 있습니다.
둘다 feature selection을 찾는 것이 맞아요.
참고사항) Linear Discriminant Analysis가 왜 feature selection ?
우리가 수업때 배웠던 예제는 2차원 feature를 갖는 두 클래스에 대한 데이터에 대한 예제였습니다.
각 feature는 저마다 한 차원씩을 갖게되는거고
그래서 2차원 좌표로 그려낼 수 있었어요.
이 때 만약 우리가 찾은 LDA 축의 방향이 x축쪽에 더 누워있으면 x라는 feature 가 y라는 feature보다 더 중요한 feature였다고 정의한셈이 됩니다.
예를 들어 이렇게요.
반대로 y축하고 더 비슷한 기울기를 갖는다고하면 그 때는 y라는 feature가 두 클래스를 분류하는 것에 더 많은 영향을 주는 feature로서 고려되었다라고 볼 수 있습니다.
PCA나 LDA는 기존의 feature와는 다른 ‘새로운 feature 축’을 찾아내는 것이므로 feature selection 기능이 있다고 말할 수 있습니다.
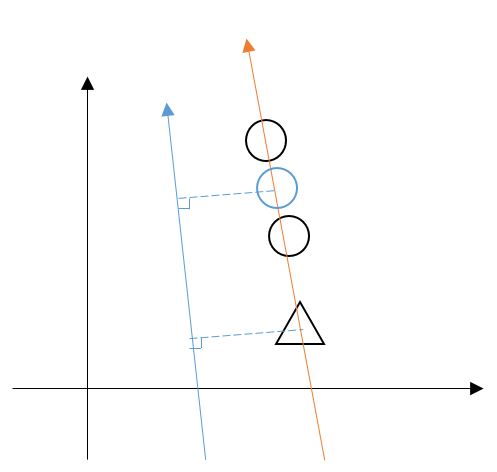
주황색 벡터는 PCA가 찾은 벡터입니다. 말 그대로 클래스가 뭐든 상관없이 모든 데이터들을 가장 잘 나타내는 벡터를 찾은 것 뿐이구요,
파란색 벡터는 LDA가 찾은 벡터입니다. 물론 평행 이동해서 데이터들을 관통하게 그릴 수도 있지만 잘 나타내보려고 띄워서 그렸는데요, LDA 알고리즘에 의해 동그라미 클래스들의 중심을 찾아 사영시켜 봤을 때, 그리고세모 클래스들의 중심을 찾아 사영시켜봤을 때 클래스별 분산은 적고 두 클래스간 간격은 크게 하는 벡터로 저 파란 축을 찾을 수 있었다는 겁니다!
Threshold는 파란 축 어딘가로 설정해 두 클래스를 잘 구분할 수 있도록 정하면 되는 거였겠죠?
이해가 되셨을 거라 생각합니다!
LDA를 바이너리 분류기에 두긴 했지만, 멀티클래스 분류기에도 충분히 사용이 가능합니다!
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!