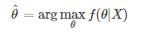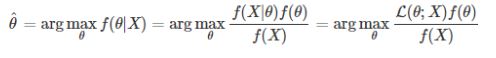MLE & MAP_Machine Learning(7)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
문제 해결 시 파라메트릭 메소드를 이용하게 될 경우 학습을 시키다는 것은 파라메터를 최적화시키는 것을 의미합니다.
여러 방법이 존재하겠지만, 이 파트에서는 MLE와 MAP를 배웁니다.
MLE(Maximum Likelihood Estimation)
MLE는 모델 파라미터를 observation(관측된 데이터값)에만 의존하여 파라미터들을 estimation하는 것을 의미합니다.
예시를 보겠습니다.
모델은 probability density function, f라고 정의하며, 모델의 파라미터는 세타(θ)라고 정의합니다.
또 observation은 X라고 칭하며 x1~xn까지 총 n개의 데이터를 가지고 있다고할 때 Likelihood는 위와 같이 정의됩니다.
Likelihood를 joint probability로 정의하고 있죠.
우리가 정의한 모델f에 의해서 주어진 파라메터, 세타가 주어져있을 때 데이터 X가 얼마나 잘 설명되고 있는가를 likelihood로 정의하고 있습니다.
식을 보면, n개의 데이터를 다시 joint probability로 나타내고 있습니다.
이 때 우리는 Likelihood를 최대화 시키는 파라메터, 세타햇을 맞추고 싶은 것 입니다.
각 데이터가 독립적이라는 가정 하에 X데이터들에 대한 함수값들을 곱하여 표현할 수 있습니다.
이 때 계산의 편의를 위해 log-likelihood가 많이 사용된다고 합니다.
마지막은 최적화를 위해 여느 때처럼 편미분하구요.
보다 직관적인 이해를 위해 다른 예제를 봅시다.
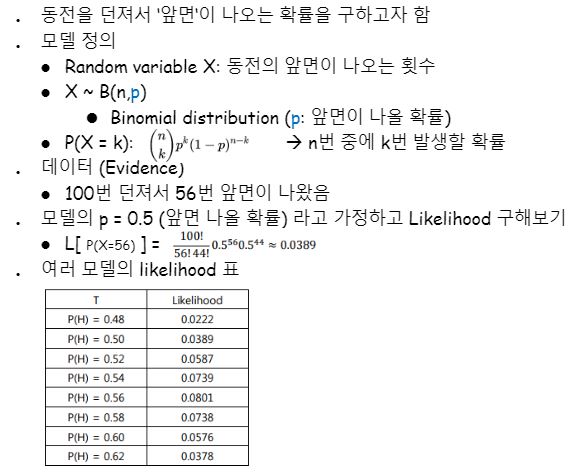
동전을 던져서 앞면이 나오는 확률을 구해봅시다.
이 때 동전은 어차피 앞면 또는 뒷면이니까 binomial distribution로 likelihood를 표기 할 수 있고, n번 던진 것 중 앞면이 나온다면 그 횟수는 X가 되는 것이고 p는 X/n으로 나온다고 이해할 수 있습니다.
n번 동전을 던졌을 때 k번 동전이 나올 횟수를 binomial distribution으로 표현한다면 P(X=k)는 저 수식이 됩니다.
동전던지기 문제에서는 전체 시행횟수 중 앞면이 나온 횟수 즉 그 비율이 “세타(=학습시킬 파라메터)”가 되는 것 입니다.
우리는 그 비율 p를 확인하기 위해 100번의 동전던지기 시행을 합니다.
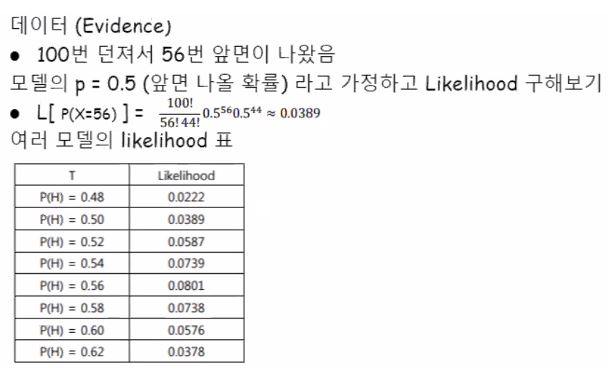
그 100번의 시행 중 56번이 앞면이 나왔다면 p를 0.56으로 두고 likelihood를 구해봅니다.
그런데 우리가 p가 0.01일 때~0.99일때까지 다 일일이 구해봐야 한다는 것을 말하려는 것이 아닙니다.
표에 보면 0.56이어야 가장 그럼직하다고 결과가 나왔지요? 일일이 한번만 나왔을 때부터 99번이 나왔을 때 이렇게 다 구하는 게 아니고요, (만약 그렇다고 하면 1000번의 시행에선 0.001부터 0.999까지…?)
아래와 같이 미분을 하여 최적의 p를 구하실 수 있습니다.
우리는 대표적인 모노토닉 함수 log를 적용한 Log likelihood를 썼기 때문에 위와 같은 식이 나왔음을 이해할 수 있습니다.
이러한 MLE는 likelihood를 최대화시킵니다.
그 말은 곧 Log likelihood값이 음수가 나올 가능성을 최소화시킨다는 말과 동일합니다.
로그함수의 그래프를 떠올려보시면 이해하실 수 있습니다.
likelihood의 값이 log함수의 인수로 들어가는 것인데, 이 인수가 커지면 음수가 나올 가능성이 최소화된다는 말이 되는 것이지요.
이러한 MLE는 likelihood를최대화시킵니다. 그 말은 곧 Log likelihood의 음수를 최소화시킨다는 말과 동일합니다.
로그함수의 그래프를 떠올려보시면 이해하실 수 있습니다.
likelihood의 값이 log함수의 인수로 들어가는 것인데, 계산 편의를 위해 사용한다 했지만 로그를 씌움으로써 음수가 나올 가능성이 열려버리는 거잖아요?
log likelihood가 음수라는 것은 어떤 의미일까요?
게다가 likelihood 역시 또 하나의 확률이니 0과 1사이의 값만을 취해야 할 텐데 로그함수는 1보다 작은 인수에서는 함수값이 음수가 나오니 말입니다.
log는 대표적인 모노토닉 함수입니다.
단순히 증가만 하기때문에 최대값을 구한다는 특성이 바뀌지 않게되지요.
likelihood의 값이 log함수의 인수로 들어갈 때, (이 인수가 커지면 음수가 나올 가능성이 최소화된다는 말이라기보다는) likelihood가 0~1사이의 값이 나오고 이 값이 log 함수의 인수로 들어가면 음수가 나오게 되는 경우가 일반적인 상황입니다.
어떤 상황에서는 1이상의 값이 인수로주어져 양수가 나올 가능성도 있다고하더라도 어쨌든, 음수로 나오게된다는 것은 최대값을 구하려던 문제가 최소값을 구하는 문제로 바뀐다는 것을 의미한다는 것을 말한 것 입니다.
앞에 있던 캡처처럼 다시 한 번 최적화 수식을 전개해보았습니다.
살펴보면 p= x/n 즉, 앞면횟수/총횟수로 앞의 표 결과와 일치하는 것을 알 수 있습니다.
즉, n=100 이고(즉, 100번 던졌고), 앞면이 56번(즉, x=56) 나왔다면,
p = 0.56 으로 곧바로 계산할 수 있습니다!
실제로 p = 0.56 일 때 likelihood가 최대가 된다는 것을 보여주기 위해서 p=.0.48~0.62 에 해당하는 likelihood 값을 표로 보여준 것 뿐이고, 앞면이 나올 확률이 p이고 binomial distribution을 따른다고 가정하고, 100번 던져서 56번 나왔다고 하면 p=56/100=0.56 일 때 가장 그럼직하다고 말할 수 있어진다는 것입니다.
이 예제를 보면 MLE는 참 직관적인 듯 보입니다.
동전던지기에 국한하여 이 문제 자체가 binomial distribution 이기 때문에 최적화식을 전개하다보니 p=x/n이라는 결과를 얻게 된 것이지 MLE를 적용하는 모든 문제에 적용되는 것이 아니며, 저마다 그 문제상황에 맞는 likelihood 식을 가지고 세타의 변화에 따라 likelihood를 최대화 시키는 세타로 estimate하기 위해 해당 likelihood를 편미분하여 편미분식=0의 과정을 거쳐줘야 합니다.
MLE는 관측데이터에 전적으로 의존하기 때문에 outlier에 민감합니다.
Cf) 아웃라이어는 잘못평가된값(극단값 또는 이상치)을 말합니다.
MAP(Maximum a Posterior Estimation)
위와 같은 MLE의 단점을 해결하고자 나온 학습 방법입니다.
수식은 아래와 같습니다.
세타와 X위치가 바뀌었죠.
이전의 P(X|parameter)같은 경우는 데이터 observation을 통해 가능하다하지만, MAP의 세타햇은 어떻게 구할까요?
MLE는 주어진 파라메터를 기반으로 데이터의 likelihood를 최대화하는 것이었다면, MAP는 주어진 데이터를 기반으로 최대확률을 갖는 파라미터를 찾습니다.
그러기 위해서는 바로 구하기 어렵기 때문에 우리가 앞서 배웠던 Bayes Theorem을 적용합니다.
MAP 수식 안에 likelihood가 들어간다는 것을 알 수 있습니다!
분모부분은 똑같으니까 분자에 대해 비례하기 때문에 뒤에 있는 두개의 텀 likelihood와 f(세타)에로부터 계산된다고 볼 수 있습니다.
앞서 말했듯이 Likelihood는 순수하게 데이터에 의존합니다.
하지만 뒷 텀 f(세터)는 사실 “사전지식”로써 파라메터 자체의 확률인거에요. 이 사전지식 p(parameter)만 주어진다면 MAP를 적용하여 MLE의 단점을 어느 정도 해결할 수 있답니다.
MAP도 최적 세타햇을 구해야 하니까 (likelihood식*parameter자체확률) 전체식을 세타로 편미분하여 최적화 시켜줘야 합니다.
예제를 보며 MLE와 MAP의 차이를 이해해봅시다.
현실세계에서는 “일부만 샘플링해서 전체사람을 추정할거야” 하는 방법을 많이 사용합니다.
그런데 10만명의 성적분포를 구할 때 10명만 샘플링하여 파라메터 평가를 수행하려고 합니다.
10명이 약 70점을 평균값으로 뭉쳐있는데, 사실 대부분의 데이터가 80점 정도를 중심으로 Gaussian을 이룬다는 경험(지식)을 가지고 있다면 MLE는 10명분의 데이터에만 의존하기 때문에 70점 근처로 결과를 얻지만, MAP는 80점 근처라는 prior knowledge를 적용하여 대략 7~80점 근처로 결과를 얻게 될 것입니다.
하지만 데이터 양이 충분히 많아지면 prior(사전지식) 값의 영향이 거의 없어진다는 연구 결과가 있습니다.
파라미터 최적화를위해서 MLE를 썼다 MAP를 썼다 할 때 위 사항을 기억하시면 될 것 같습니다.
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!