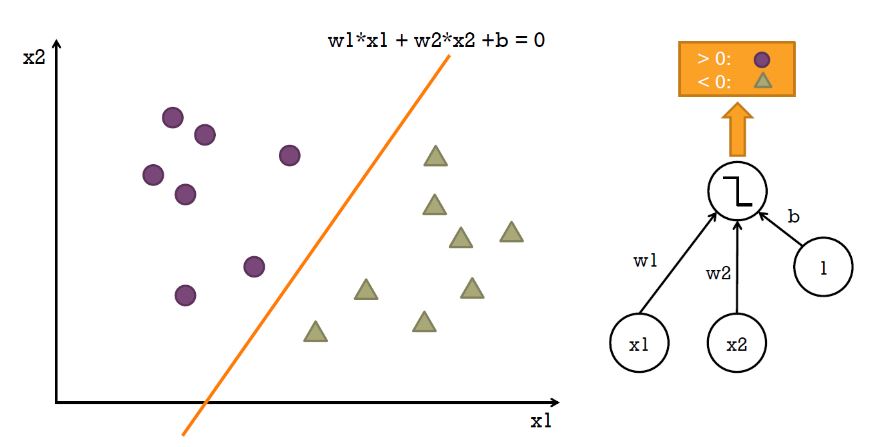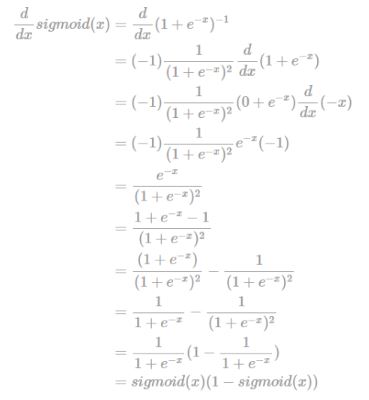Artificial Neural Network_Machine Learning(9)

Intro

학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.

기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.

gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.

• 원격 실습환경구축 따라하기
  

• Machine Learning(1) 포스트 보러가기
  

• Machine Learning(2) 포스트 보러가기
  

• Machine Learning(3) 포스트 보러가기
  

• Machine Learning(4) 포스트 보러가기
  

• Machine Learning(5) 포스트 보러가기
  

• Machine Learning(6) 포스트 보러가기
  

• Machine Learning(7) 포스트 보러가기
  

• Machine Learning(8) 포스트 보러가기
  

• Machine Learning(10) 포스트 보러가기
  

이번 시간에는 지난 시간 배웠던 퍼셉트론을 기반으로 ANN, 인공신경망을 배웁니다.

ANN(Artificial Neural Network)

Neural Network를 우리말로는 신경망이라고 부릅니다.
ANN은 뇌세포를 본따 만들어진 ‘퍼셉트론’으로 이루어진 네트워크입니다.
그리고 사람이 만든 뉴런들의 네트워크입니다. 그래서 인공신경망이라고 말합니다.

중요한 특징들이 있습니다.
첫째로는 블랙박스같다는 것이죠. 그래서 의사결정나무처럼 명확한 의사결정 규칙이 보이지 않지만 많은 분야에서 훌륭한 성능을 보이고 있습니다.

중요한 특징 두번째는 feed-forward로, 한 쪽 방향으로 흘러간다는 것입니다.
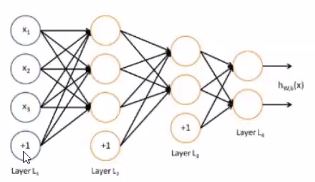
보통 1개 이상의 hidden layer를 갖습니다.
hidden layer의 개수가 많을 수록 deep한 neural network가 되는 것입니다.
딥러닝이라는 말도 여기서 파생된것이지요.

하나하나의 노드가 퍼센트론이라고 보시면됩니다
. 그리고 각 층들의 입장에서봣을때 좌우에 있는 모든노드들과 연결된것을 fully connected이다라고 말합니다.

그리고 같은 층 사이에는 연결이없는데 이러한 그래프를 bi-partite graph라고 합니다.

입력이있고 출력이 있는 것은 알겠는데 이 hidden layer는 무엇일까요?
질문을 바꿔서 입력에서 바로 출력으로 간다면 어떤 문제가 있을까요?
지난시간 잠시 보았던 것처럼 XOR와 같은 비선형 문제를 풀 수 없습니다. 단순한 선형 문제만을 풀 수 있어지죠.
이러한 단층 퍼셉트론의 선형문제만을 풀지못한다는 단점을 이슈화해서 머신러닝의 암흑기가 찾아오기도했었지요.

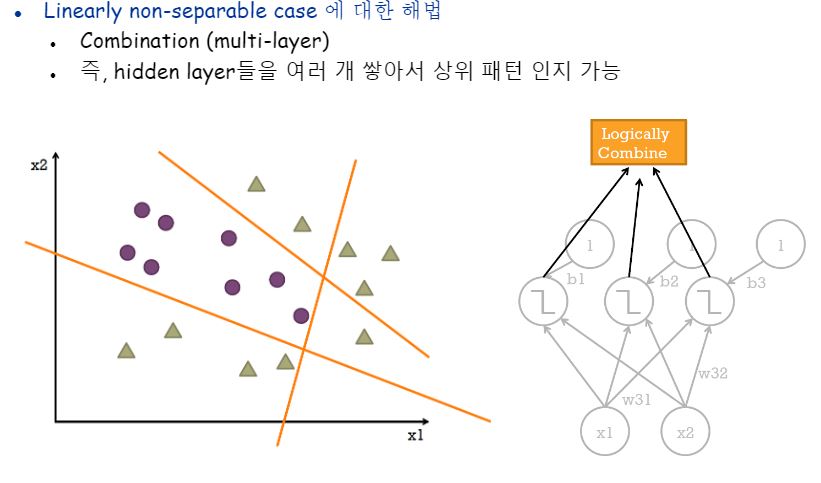
멀티레이어 네트워크는 한층한층 오른쪽으로 갈수록 즉 출력층으로 갈수록 모종의 집약된 또는 점점 더 고도화된 정보만을 보고 판단하는 것으로, 비선형 문제 해결에 접근할 수 있습니다.
선형으로 분류가 안되는 케이스는 단층이 아닌 다층 신경망을 적용하면 해결이 가능합니다.
모델이 고차원의 패턴을 인지할 수 있는 것입니다.

Activaiton Function

하지만 multi-layer이기만 하면 될까요?
linear한 것들을 통합하는 함수가 여전히 linear하다면 linear한 것들을 아무리 여러개 모아봤자 소용이 없어집니다.
선형대수학적으로 이야기를 하자면 같은 차원끼리 덧/뺄셈을 해봤자 그 벡터의 차원이 달라지지 않는 것과 같습니다.
그래서 활성화함수(activation function)을 바꿔줄 필요가 있습니다.

선형합을 한 다음 비선형패턴도 풀어낼 수 있는 비선형함수를 활성화함수로서 사용해주어 해결합니다.
하지만 아무함수라고 다 되는것이 아니라 최적화를 위해 미분가능한 함수여야 합니다.

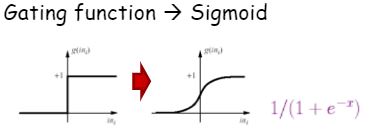
대표적인 활성화함수가 sigmoid입니다. 선형 활성함수로 썼던 gating function과 굉장히 비슷한 트렌드를 갖습니다.

ANN을 분류문제에서 사용하는 경우 때문에 hidden layer에서는 sigmoid를 사용하고, output layer에서는 softmax function을 많이 사용합니다.
참고로 회귀문제에서는 f(x)=x 를 사용합니다.

softmax는 각 노드(출력층의 모든 노드는 각 클래스가 될 것임)에 대한 확률값을 주게 됩니다.

하지만 multi label 문제 해결에는 소프트맥스는 적적하지 않습니다.
그럴 때는 시그모이드를 아웃풋레이어에 사용하는 것이 더 낫기도 합니다.

이 소프트맥스함수는 지수함수이다보니 컴퓨터가 계산하다보면 오버플로우가 발생할 우려가 있습니다.
그래서 개선식을 사용하곤합니다.

활성함수의 입력값으로 사용되는 가중합(weighted sum)을 하는 이유는 무엇일까요? 그냥 더하면 안되는 걸까요? bias의 역할은 무엇일까요?

더 중요하고 덜 중요한 애들을 구분하여 더 똑똑한 결정을하기위해 가중치를 두는 작업의 핵심요소가 바로 weight입니다.

물론 은닉층에서의 각 노드가 무슨 역할일지 설명이 불가능하여 엔지니어가 직접 weight를 조정하기가 어려운 것이 사실이지만, 놀랍게도 ANN에서 학습이 진행되면서 정체가 뭔진 모르겠지만 특정 노드에 있어서 가장 적절한 weight를 찾아주게 됩니다.
이 말을 고급지게 표현하면 feature를 자동으로 학습한다 라고 표현할 수 있습니다.

노드 자체에 대한 중요도 즉 prior 정보를 주기 위해 사용하는 것이 bias입니다.

bias 역시 weight처럼 개선되게 됩니다.
wx+b로 표기하게 되니까 bias도 선형합을 할 때 함께 개선됩니다.

우리는 여태 배운 다른 분류기 머신러닝 모델을 적용할 때 feature 정의를 해주게됩니다.
sift니 surf(speeded up robust features)니 하는 feature를 예쁘게 뽑아내줄 툴도 개발이 되어있습니다.
이미지 데이터라고 하면 밝기 조절도 좀 해줘야하고 노출값도 만져줘야하고 그런 과정이 필요한 것이지요.

속된말로는 머신러닝 모델이 좋은 성능을 낼 수 있게 하게 엄청 노력해서 떠먹여줘야하는거에요.
그런데 딥러닝 모델은 (물론 떠먹여줘도되지만) 숟가락만 줘도 알아서 떠먹습니다.

하지만 왜 그런 결과가 나왔는지 설명할 수는 없지요..
explainable한 AI model 을 만드는 것이 현재 AI 세계의 공통 목표라고도 할 수 있습니다.

Weight Matrix and Bias

우리가 ANN을 쓰는 이유를 다시 상기시켜봅시다.
“패턴인지”였지요 그러려면 “패턴 학습”이 필요할 것인데, 학습이 되는 것은 뭘까요?
바로 각 층사이를 잇는 weight matrix입니다.
그리고 각 층의 bias 까지요!

1. weight matrix 의미와 역할 두 개 층의 각 노드쌍 사이의 관계 중요도입니다.
   해당 노드쌍이 함께 등장한 빈도수(두 노드가 관측 가능한 경우)에 기반합니다.
   

2. bias 의미와 역할 각 노드 자체의 중요도로 해당 노드 빈도수(해당 노드가 관측 가능한 경우)에 기반합니다.
   

Backpropagation

관측가능한 값은 모델 특성상 Input, Output layer에만 존재하므로, 먼거리(?)에 놓인 이 두 개의 Layer 사이의 Co-occurrence 를 기반으로 weight matrix, bias들을 학습할 방법이 필요합니다.

ANN의 한계라고 할 수 있지요.
아래 캡처에서 알 수 있듯이 단순한 모델은 한번에 가능해요.

ANN 모델 파라미터는 이런식으로 학습할 수는 없을까요?

층이 깊어질 수록 성능이 더 좋다는 연구 결과가 있습니다.
하지만 바로 편미분을 하는건 네트워크가 깊어지면 깊어질수록 매우 어려워지겠지요?

그래서 수학적 체인룰을 적용합니다.
backpropagation 알고리즘이라고 부릅니다.

고등학교 이과수학 커리에서 배우셨을거에요.

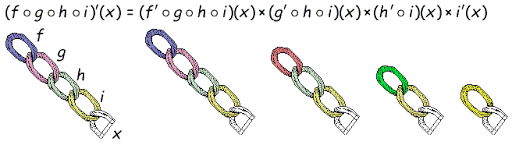
MSE는 Mean Squared Error이며, 교차엔트로피 오차는 CSE(Cost Entropy Error)입니다.

하지만 층이 너무나 깊게 형성되어있으면 역전파시에 1 이하의 값들이 곱해지다 보니 그라디언트 값이 입력층으로 갈수록 너무 미미해집니다.
이 현상을 gradient vanish라고 합니다.

이러한 문제들이 있다보니까 어떻게 더 효율적으로 층을 깊게 쌓을지에 대한 많은 연구들이 진행되고 있습니다.

지금 배우는 Neural Network는 아주 중요해서 여태까지 배운 내용을 짧게 복습해보겠습니다.

Activation function은 선형모델에 쓰면 안되고, 또 미분가능해야 합니다.
그런 함수 중 대표적인 함수가 지난 시간에 배웠던 sigmoid입니다.

회귀문제는 f(x)=x라는 identical function을 쓰지만 분류는 softmax를 많이 씁니다. 하지만 멀티레이블은 sigmoid를 써야 합니다.

Softmax를 간단히 정리하자면 각각의 output layer에서의 나올 수 있는 노드별 선형 합들 중에서 “내가 쟤보단 더 나아”하는 랭킹 매기기에요.
제일 그럼직한 놈 하나만 뽑을 거면 의미가 있지만 모자를 썼는지 반지는 꼈는지 목도리도 했는지 여부를 확인해야 하는 멀티레이블 문제에 있어서 등수를 매기는 건 의미가 없지요.
그러니 멀티레이블 문제에는 softmax를 쓰면 안되는 거에요.

결국 정리하면 output layer에 어떤 함수를 쓸지는 신중히 결정해야 하는 문제라는 것입니다.

우리가 흔히 풀게 될 문제는 멀티 레이블이 아니라서 softmax를 많이 사용하게 되는데, 오버플로우 문제를 해결하기 위해서 개선식을 쓰구요.
식의 모양새를 보면 알 수 있듯이 앞서 배웠던 다항 로지스틱 회귀와 softmax는 절친입니다.

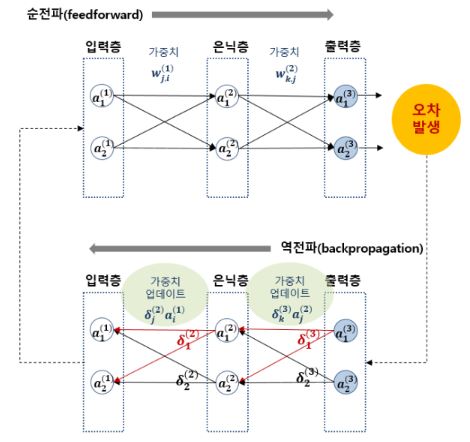
Output layer에서 발생했던 error(즉, loss)를 가지고 신경망을 (정확히는 w등의 파라메터를) 개선을 해야 하는데 이 때 쓰이는 방법이 바로 backpropagation입니다.

원래 결과를 뽑아낼 때에는 왼쪽에서 오른쪽으로 feed-forward 흐름을 탔었다면 개선할 때에는 거꾸로 오른쪽부터 왼쪽으로, 정확히 말하자면 출력층에서 입력층 방향으로 전파되면서 계산해나가는 것이죠.

Cost function에서 loss파트에서는 MSE와 CSE가 잘 사용됩니다.
오차의 제곱들의 평균을 구하는 방식이 MSE이며, 예측값과 정답값을 엔트로피로 함께 표현하는 방식이 CSE입니다.

Cost function

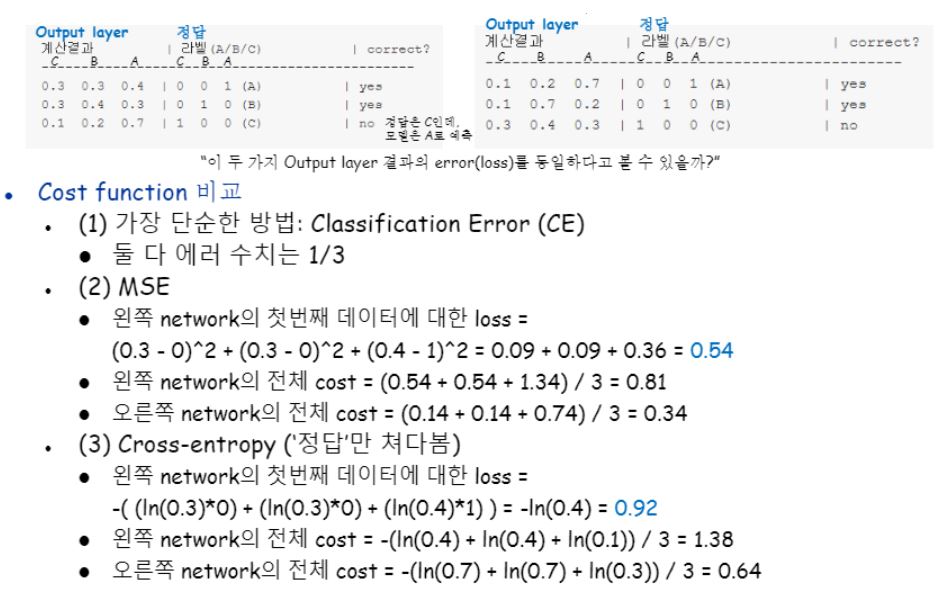
두 개의 별개의 네트워크의 output layer가 아래와 같다고 가정합니다.

첫 번째 데이터에 대한 결과물로 output레이어에 노드가 세 개 있었는데 c0.3 b0.3 a0.4로 나왔습니다.
정답은 c0b0a1이라는 one-hot vector로 표현하고 있어요.
그렇다면 어쨌든 a가 가장 그럼직하니까 정답은 맞은 거죠?

같은 방식으로 두 번째, 세 번째 데이터도 확인해보았을 때, 세 번째 데이터는 정답과 예측값 사이의 차이가 생겼네요!

이어서 바로 옆의 또 다른 네트워크도 확인해봅시다.
첫 번째 네트워크와 비교하여 상대적으로 아쉬운 차이(?)로 세 번째 데이터에 대한 예측이 틀렸네요!

그렇다면 두 네트워크 모두 첫 번째와 두 번째 데이터에 대한 예측은 맞았고 세 번째만 틀린건데 두 네트워크의 error가 같다고 말할 수 있을까요?

위 질문에 그렇다, 같다고 할 수 있으려면 CE(classification error)라는 가장 단순한 방식으로 loss를 표기한 것입니다.

여기에서 우리가 앞에서 배웠던 loss 함수인 MSE와 CSE를 사용하게 되면, “엄밀히 말하면 오른쪽 네트워크가 조금이라도 더 성능이 높은 거지!” 라고 말할 수 있어지는 겁니다.

또한 위 예제에서 볼 수 있듯이 원핫벡터에 CSE를 적용하게 되면 정답이 아닌 애들은 0이 곱해지면서 없어집니다.
이는 다시 말해 CSE는 “정답”에 해당하는 노드만 바라보게 된다는 특징을 갖는다고 말할 수 있습니다.
좋다, 나쁘다는 지금 평가할 수 있는 것은 아니에요.

Training

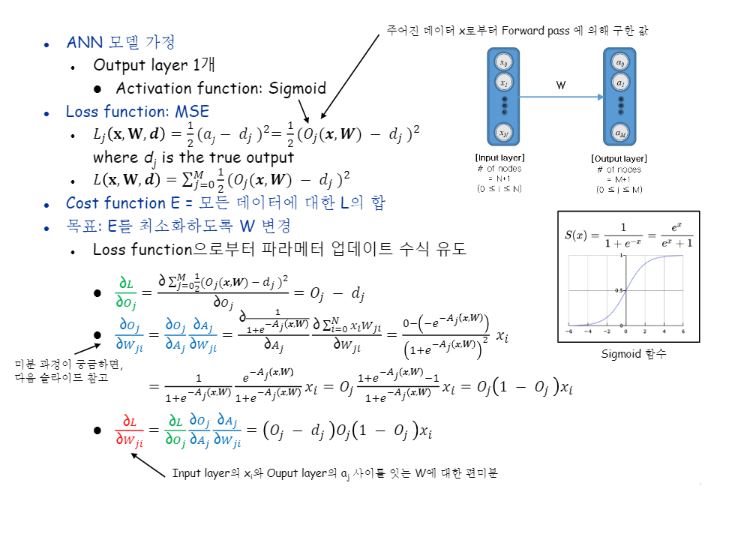
이해를 용이하게 하기 위하여 은닉층 없이 두 레이어 사이의 오류 전파를 보겠습니다.

식에서 d는 정답을 말하고 O는 sigmoid를 거쳐서 나온 실제 값을 말합니다.
뺀 값은 결국 오차를 의미하며 오차는 우리가 최소화해야할 대상이 되지요.
우리에게 익숙한 편미분을 통해 최적화시키려고 하니 문제가 하나 있네요!
w에 대해 loss를 편미분하고 싶지만, 활성화 함수를 거친다는 특성 상 w값이 바로 보이지 않기 때문에 chain rule을 적용해서 즉, sigmoid 식을 통해서 그라디언트를 구해줘야 합니다.
참고로 위의 식은 MSE를 쓰기 때문에 나온 식이에요.
Loss function과 Activation function을 무엇을 쓰는 가에 따라 식이 많이 달라지겠죠?

마지막 정리된 식을 한 번 봅시다. 이 식이 직관적으로 설명이 가능하길 바라는 마음으로요.

O-d는 앞서 설명했듯이 에러를 의미하는 거에요. 에러가 크면 더 많이 변해야 된다는 것을 의미하죠. 그럼 두 번째 텀과 세 번째 텀은 뭘까요?

O는 활성화함수를 거쳐서 나온 값이므로 0~1사이의 값을 갖는데, 그 값이 0.5에 가까워질수록 두번째 세 번째 곱 결과가 커지고, 양극단으로 갈수록 그 값은 작아지는 특성을 갖습니다.
입력 값이 컸다면 w가 개선되는 양도 커져야 감당이 가능할 거라고 보고 비례하도록 곱 해주는 거죠.

즉 네 번째 텀인 입력값과 오차의 크기에 비례해서 개선해주겠단 뜻입니다.

잘 이해가 안되셨다면, 이렇게 설명을 한 번 해보겠습니다.

가운데(0.5)에 있을수록 “결정 장애”인거죠? 확확 변해줘야 한다고, 그런 중립기어로는 얻을 정보가 없다고 판단하는 거에요.
혹시 sigmoid 미분 쪽 수식이 잘 이해 안 된다면 그 다음 슬라이드를 보시면 이해에 용이할 겁니다.

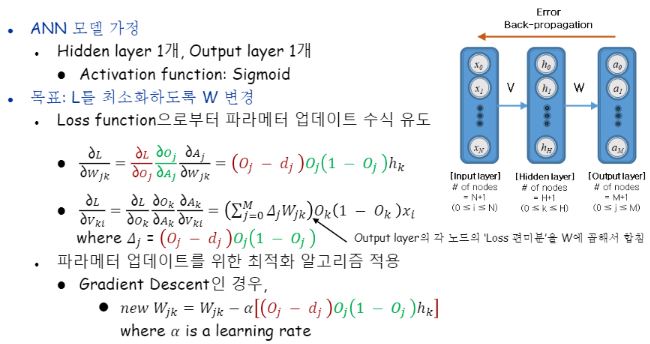
이제 input과 hidden과 output layer를 갖는 네트워크도 봐봅시다.

첫 번째 수식인 Output-hidden 사이의 그라디언트 구하기는 이해가 되실 거에요. 똑같습니다 직전 예제와!

가장 오른 쪽 층인 출력층에서 바로 직전 은닉층 사이에서 일어나는 일이며, 가장 먼저 간선들의 가중치들을 갱신해줍니다.

그 다음이 문제입니다. 한 층 건너와서 Input과 hidden사이요.
식에서 사용된 ‘델타’가 무엇인지 먼저 정의해줄 필요가 있습니다.
델타j라함은 j번째 노드 자체에 대해서 발생했던 error자체라고 볼 수 있어요.

거기에 Wjk를 곱한다는 것은 이어주는 간선을 곱해줌으로써 우리가 구하고자 하는 게 Vki라고햇을때 hidden layer의 k번째 노드에 대해서 backpropagation을 할 때 forwarding 시 자신이 영향을 줬던 모든 output layer의 노드들로부터 피드백을 받는 걸 뜻합니다.

hidden layer의 k번째 노드랑 연결되었던 output layer의 모든 노드들 하고 그 각각을 잇고 있던 간선들까지 모두 곱해서 summation해서 받는 거지요.
“내 오류가 이렇게 나온 데에는 너도 책임이 있어”라는 의미로 해석할 수도 있겠네요.

전체 네트워크가 n개의 층으로 이루어져있다고 할 때 loss함수에 체인룰을 적용하여 편미분함으로써 n-1번째 층(은닉층)의 각 노드들의 입력값과 오차의 크기에 비례하여 출력층과 n-1번째 층(은닉층) 사이의 간선들의 가중치를 먼저 개선시키고,
n-2번째 층(은닉층)의 각 노드들의 입력값과 출력층의 각 노드의 편미분값과 해당 노드를 잇는 간선의 가중치의 선형합의 크기에 비례하여 n-1번째 층(은닉층)과 n-2번째 층(은닉층) 사이의 간선들의 가중치를 개선시키고,
n-3번째 층(은닉층)의 각 노드들의 입력값과 n-2번째 층(은닉층)의 각 노드의 편미분값과 해당 노드를 잇는 간선의 가중치의 선형합의 크기에 비례하여 n-2번째 층(은닉층)과 n-3번째 층(은닉층) 사이의 간선들의 가중치를 개선시키고,
…,
입력층의 각 노드들의 입력값과 2번째 층(은닉층)의 각 노드의 편미분값과 해당 노드를 잇는 간선의 가중치의 선형합의 크기에 비례하여 2번째 층(은닉층)과 입력층 사이의 간선들의 가중치를 개선시킵니다.

그 다음 개선된 네트워크에 다시 데이터를 입력시켜 실제 값을 뽑아내지요.

위 과정을 반복하여 계속해서 네트워크를 갱신시킵니다.
그래서 iterative learning이라고 말합니다.

그리고 이 때 갱신하는 데 사용될 최적화 알고리즘은 보통 Gradient Descent로 먼저 입문합니다.

여기서 다시 한 번 전반적인 내용을 정리해봅시다.

활성화함수로 선형함수를 사용해서는 안된다고했고 그래서 sigmoid를 배웠지만 reLU도 요즘 많이 사용됩니다.
그리고 멀티레이블이 아닌 경우에는 끝층에 softmax가 많이 사용된다는 것을 배웠습니다.

Naïve bayes에서의 파라미터는 뭐였죠? 바로 likelihood와 prior였죠.
ANN에서의 파라메터는 weight죠.
Feed forward로 신경망을 쭉 돌고나서 나온 예측값과 정답값 간의 loss를 정의해서 신경망의 가중치를 갱신시키죠. 그렇게가 한번의 epoch이 되는데 이렇게 하고 나서 끝이 아니라 다시 여러 번 반복해줘야 합니다.
한 발자국 만에 산정상에서 나올 수 없으니까요.

loss를 정의할 때 backpropagation에서 MSE나 CEE를 이용하는 경우가 많다고 배웠습니다.
그리고 sigmoid 를 활성화함수로, MSE 를 손실함수로 두었을 때의 그라디언트 디센트에 의한 학습 예제를 살펴보았습니다.

optimization이라는 것은 모델 자체에서의 최적화해야할 대상을 선정하고 우리의 목적에 맞게 최소화를 하거나 최대화를 하는 것을 말합니다.

최적화 알고리즘도 여러가지가 있습니다.
앞서 배웠던 GD의 경우는 Learning rate를 오차함수의 그라디언트에 곱해서 그만큼을 빼주어 개선하는 방식이었지만, 다른 최적화 알고리즘은 저마다의 방법이 있습니다.

GD는 Batch GD와 Stochastic GD 등으로 나뉘며, 또 GD 말고도 여러 최적화 알고리즘이 있습니다.

• Adagrad
  
• Adadelta
  
• Adam’s optimizer(많이 사용됨)
  
• Momentum
  
• RMSProp
  
• …etc
  

여기서 batch gd는 학습 data가 n개 있을 때 n개 전체에 대한 gradient를 적용하는 것을 말합니다.
Stochastic gd는 학습 data n개 각각에 대한 gradient를 적용하는 것을 말하며, mini batch gd는 학습 data n개를 작은 mini batch들로 쪼개서 gradient를 적용하는 것을 말합니다.
Stochastic GD는 데이터 개수만큼 각각에 대한 gradient를 적용하는 것이기 때문에 아주 오래걸립니다.
전체 데이터 N개 데이터를 한번에 메모리에 올리려고한다면 자원이 모자를 수 있겠지요. 그래서 mini-batch를 많이 사용합니다.

Batch 크기가 크다면 그만큼 빠르게 학습이 진행되겠지만 컴퓨팅 리소스가 부족하다면 batch를 적절히 조정해줘야겠지요.

그렇다면 시간에만 차이가 있지 결과는 똑같을까요? 그렇지도 않습니다.

mini batch는 Batch gd와 조금 다른 결과를 낼 수 있지만 비교적 빠른 속도로 학습되며, 여러 iteration을 거치면 Batch GD와 유사한 결과를 낸다고 알려져 있어 실제로도 많이 쓰이는 것입니다!

Batch를 작게 해야 좋다하는 분들도 계시고 크게 해야 좋다는 분들도 계시며, 처음엔 크게하다가 뒤로가면 갈수록 batch크기를 작게 해줘야 한다라는 분들도 계십니다. 이에 대한 연구는 On going 상태에요.

점점 작게해줘야한다라는 것을 learning rate decay라고 합니다.(weight decay와는 다릅니다)

학습 데이터에서 학습이 잘 된다해서 test에서도 잘 될 거라는 보장이 없으므로 validation 데이터에 대해서도 똑같이 loss를 구해주어야 합니다.

최적화 알고리즘들은 많지만 핵심은 뭐냐면 글로벌 optimizer를 구하긴 매우 어렵다는 것입니다.
Loss의 형태가 우리가 원하는 이상적인 convex 모양이 아닌 것이죠.

항상 글로벌 옵티마를 구한다는 보장을 하는 알고리즘은 아직까지 구해지지 않았습니다.

Adagrad랑 adam’s optimizer는 많이 사용되니 알아둘 필요가 있습니다.
최적화 기법에 대한 자세한 정리가 실린 포스팅의 링크를 여기에 걸어드리겠습니다.

ANN 전처리 & 초기값

입력될 데이터의 각 Feature 값을 scaling합니다.

• 정규화(normalization) : 0~1로 변환하는 것을 말합니다.
  
• 표준화(standardization) : Normal 분포를 따르도록 변환하는 것을 말합니다.
  

파라메터(layer간의 weight matrix) 초기값 설정에 관한 방법입니다.
어떤 값으로 초기화하느냐에 따라 학습에 소요되는 시간도, 성능도 달라질 테니까요.

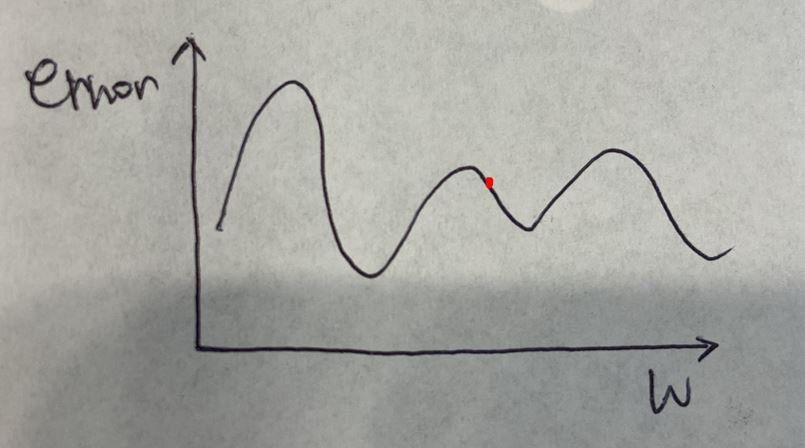
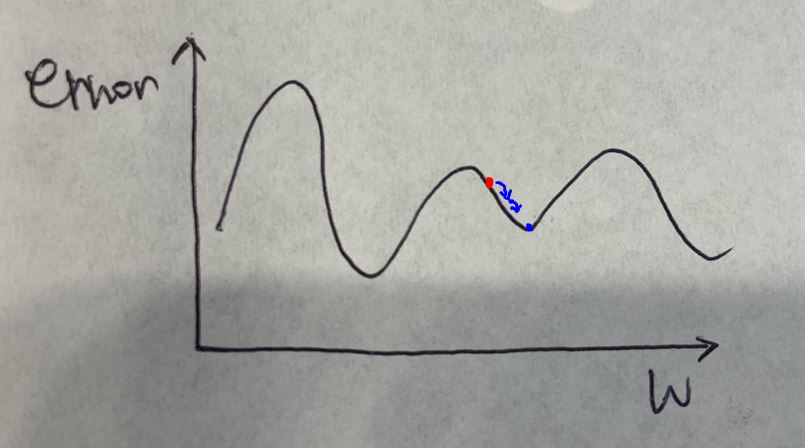
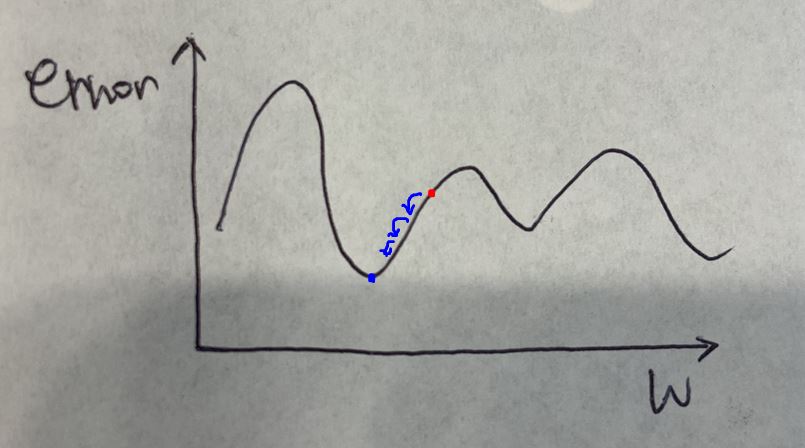
만약 저 곳이 초기값으로 주어졌다면 여러번의 epoch 후에는 아래와 같이 최적화가 될 것입니다.

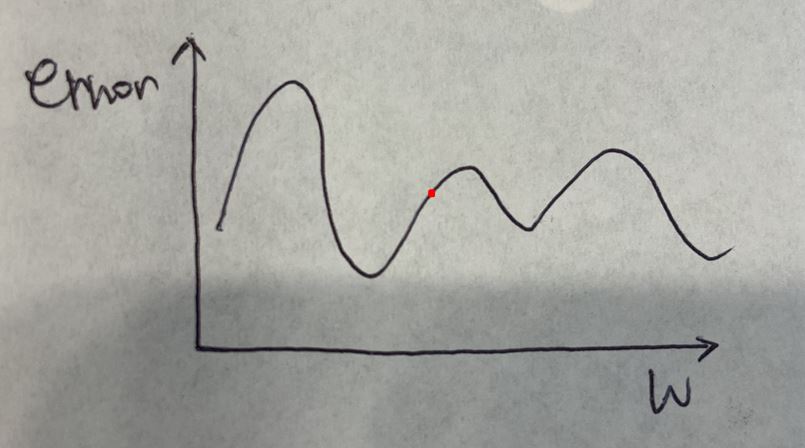
만약 아래와 같이 초기값으로 주어졌다면 여러번의 epoch 후에는

아래와 같이 최적화가 될 것입니다.

글로벌 최대값이라는 것을 찾지 못하기 때문에 그렇습니다.
저 고개 너머에 어떤 곳이 있을지 알수가 없기 때문이에요.

초기값을 선정하는 문제 역시 여러 방법이 있습니다.

Normal(0,0.01^2) 방법의 문제점은 어렵게 써있는데, 쉽게 말하자면 학습이 진행됨에 따라 신경망에 한쪽만 영향을 많이 받고 그외의 쪽에는 입력층으로부터 얻어오는 정보가 매우 적어지는 이상결과를 갖고 올 수 있습니다.
자비어나 He 초기화 방법이 많이 사용된다고 합니다.

실전 학습 기법

Learning rate는 보폭이라고 생각하시면 편합니다 너무 보폭이 작으면 학습이 지나치게 오래걸리며, 경우에 따라 과적합 우려가 있으며 너무 크면 파라메터 값들이 최적으로 수렴되질 않고 발산해버려 학습에 실패할 수 있습니다.

적당한 값을 찾아줄 필요가 있지요.

ANN 모델에서도 오버피팅 문제가 발생할 수 있습니다.

오버피팅이 무엇이었나요?
데이터에 비해 모델이 복잡한 경우라고도 말할 수 있어요.
그렇기 때문에 데이터를 늘려주거나 아님 모델 복잡도를 줄이거나 하는 등의 방법으로 해결을 할 수 있는데요, 모델을 줄이려면 어떻게 해야할까요?

첫 번째로는 Feature를 줄여보는 것입니다. 두 번째로는 각 층의 노드개수나 층의 개수를 줄이는 방법도 있습니다.
노드 개수 같은 것들은 ANN 모델에 있어서 hyper parameter인데, 이들을 적절히 결정해줌으로써 오버피팅을 막을 수 있다는 말입니다.
또한 epoch 횟수도 너무 크면 오버피팅이 되는 경우도 있기 때문에 너무 오래 학습을 시키지 않아야하는 경우도 있습니다.
그럴 경우에는 엔지니어가 정해놓은 일정 threshold 이하로 cost가 떨어지면 학습이 중단되도록 코드를 짜면 됩니다.

Hyper parameter 튜닝 방법으로는 무식하게는 Grid search 부터 Random search, 그리고 자동으로 네트워크를 만들어줄 수 있는 Neural architecture search 등이 있습니다.

또 다른 오버피팅 예방법으로는 선형회귀 때 잠시 배웠던 정규화방법이 있습니다.
L1과 L2 정규화가 batch GD의 수식에 사용될 수 있습니다.

앞에서 먼저 배웠던 learning rate decay는 점점 갱신 보폭의 크기를 줄여나가는 것을 말하는 개념적인 용어이고, weight decay는 w가 너무 커져 overfitting을 예방하기 위해 곱해주는 상수값을 말합니다. L2 정규화를 하면 자연스럽게 weight decay 가 되는 거에요.

L1은 L2처럼 식전개과정에서 weight decay는 나오진 않지만 w를 줄여주는 효과는 있습니다.(그래서 weight decay 효과를 가지고 있다고 말하기도 합니다.) L2가 아닌 다른 정규화기법에서도 weight decay가 나올수도 있습니다.

Incremental Learning

이전에 학습되어있던 모델에 새로운 데이터를 추가 학습시키는 것을 말합니다.
미니배치로 데이터를 쪼개서 학습시킬 수 있다면 새로운 데이터로 추가학습은 왜 안되겠어요! 가능합니다.

뉴럴네트워크가 아닌 다른 모델들 중에는 이러한 incremental learning이 안되는 경우가 있습니다.
이어서 학습이 안되어서 데이터 A와 새 데이터 B를 합쳐서 아예 새로운 모델을 만들어줘야하는 경우가 있습니다. 꽤 많습니다.
하지만 ANN은 Incremental 하게 할 수있습니다.

심지어 전혀 다른 데이터를 통해 학습한 모델에 대해서도 유의미한 이득을 얻는 사례도 소개된 바가 있습니다. 이를 전이학습(transfer learning)이라고 합니다.

예를 들어 한국어에서 영어로 번역해주는 신경망을 모델링해서 이미 그 가중치들도 학습이 되어있는 상태라고 합시다.
이번엔 한국어에서 프랑스어로 번역해주는 신경망을 새로 만드는 데 이전에 한국어-영어 번역 신경망에서 학습시켜놓은 가중치정보를 그대로 가져와 초기 가중치값으로 한국어-프랑스어 신경망에서 사용하는 것이죠. 놀랍게도 더 성능이 높은 결과를 얻기도 한다는 말을 하는 것입니다.

사람도 그렇잖아요? 다른 곳에서의 지식으로부터 더 잘할수 있는 것이죠.

Auto Encoder

Neural Network는 보통 supervise learning으로 학습되지만, AutoEncoder는 unspervised learning입니다.
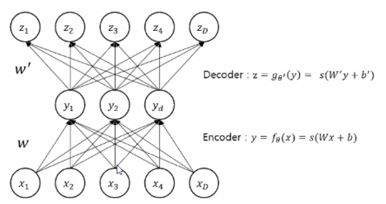
Auto Encoder의 기본구조는 아래와 같습니다.

Input을 Label로 활용하는 형태인데요, Input 을 reconstruction하는 목적입니다. 즉 f(x)=x를 학습하는 것인데요, 입력이 출력이 다시 나오게 하는 것이 무슨 의미가 있을까 싶으실 수 있습니다. 힌트는 가운데 층에 있습니다.

이미지 상의 노이즈를 제공하는 용도 들로 보통 사용이 됩니다.

Deep Learning

딥러닝은 ‘깊은 층’을 가진 neural network로 이론상 모든 종류의 복잡한 비선형 패턴을 잡아낼 수 있다합니다.
깊은 층을 가짐으로써 ‘상위 패턴’들을 모델링하는 것이 가능해집니다.

은닉층(hidden layer)를 여러개 쌓는 것이 가장 기본적인 딥러닝 모델입니다.

Deep Neural Network의 기초가 되었던 모델들로는 Restricted Boltzmann Machines(RBM)과 Deep Belief Networks(DBN) 등이 있습니다.
RBM은 1986년 Paul Smolensky에 의해 만들어졌으며, DBN은 2009년 Geoffrey Hinton에 의해 만들어졌습니다.

Convolutional Neural Network

CNN도 ‘깊은 층’을 가졌지만, convolution에 무게를 둡니다.

구조상 주된 특징으로는 Convolutional Layer(지역적인 특징을 추출)와 Pooling Layer(주요 특징만 선택하는 용도)가 있습니다.

CNN에 관련된 설명은 이전에 자세히 정리해두었기때문에 여기에 링크를 걸어놓겠습니다.

Recurrent Neural Network

순차적인 패턴을 잡아내기 위한 모델입니다.
구조상 주된 특징으로는 재귀적으로 출력에서 다시 입력으로 간다는 점인데요, RNN의 기초가 되었던 모델들은 Elman type과 Jordan type이 있습니다.

최신기법들로는 유명한 LSTM과 GRU 등이 있습니다.

Generative Adversarial Networks(GAN)

이로적으로 딥러닝 모델에 국한되는 것은 아니지만, 딥러닝 모델에 적용됩니다.

GAN 모델의 기본 개념은 아래와 같습니다. 예제와 함께 설명해보겠습니다.

• Generator : 위조 지폐 생산자에 해당하며 더 잘 속이기 위해 끊임없이 위조방법을 개선합니다.
  
• Discriminator : 위조 지폐 감별사에 해당하며 끊임없이 감별하는 방법을 개선합니다.
  

결과적으로 더이상 감별하는 것이 불가능할 만큼 완벽한 위조 지폐가 생산되는 것을 가정합니다.

개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!