Topic Modeling_Machine Learning(15)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
이번 시간에는 Topic Modeling, LDA를 배웁니다.
LDA(Latent Dirichlet Allocation)
딥러닝 모델 중에서 CNN(Convolutional Neural Network)라는 모델이 있는데 이 모델은 주된 타겟이 바로 이미지 데이터입니다.
오늘 배우게 되는 Topic Modeling은 바로 텍스트에 많이 사용되는 모델입니다.
영상에도 쓸수 있긴해요.
그렇기 때문에 기술을 잘 알고 있어야합니다.
사람들은 문서를 읽으면 기본적으로 그 문서의 주제를 파악하려고 합니다.
토픽모델링을 위한 데이터가 있다면, 그 문서를 읽고 사람은 “아 이 문서는 OO에 관한 것이네”라고 알 수 있거든요.
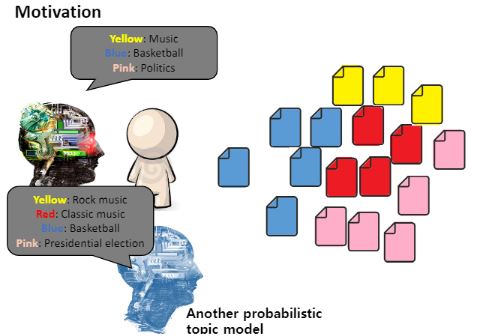
그런데 엄청나게 많은 문서가 있다고 하면 언제 다 읽겠어요? 이 것이 motivation이 됩니다.
이를 대신 해주기 위한 모델이 바로 Topic Model입니다.
그런데 토픽모델들끼리도 같은 데이터를 주더라도 파라메터를 어떻게 주느냐에 따라 서로 다르게 결과를 줄 수 있어요.
토픽모델도 일종의 클러스터입니다.
클러스터 수가 3개로 설정되느냐 4개로 설정되느냐에 따라 결과가 달라졌던 것처럼 토픽모델도 마찬가지 입니다.
즉, 모델이 달라지게 되면 보는 관점이 달라지게 되고, 서로 다른 토픽모델이 서로 다르게 카테고리화를 하게 된다 하면 어떤 모델이 더 옳은 결과를 냈는가에 대해서는 결국 그 끝에는 사람이 선택하게 됩니다.
그런데 결정까지도 자동으로 해주는 기술도 나왔다고 합니다.
그런데 그 결정도 마찬가지에요. 그 결정을 자동으로 하기 위해 또 다른 방법으로 막아세운다고하면 거기에 대해서 사람이 또 결정해줘야해요.
세상에 공짜는 없습니다..
어쨌든 좀더 디테일하게 살펴보도록 하겠습니다.
우리는 LDA에 대해 배울 것입니다. LDA란 것은 이전에 앞서 배웠던 Linear Discriminant Analysis가 아니고 Latent Dirichlet Allocation입니다.
2003년에 처음 소개된 기술이지만 그 이전에 근거가 있습니다. 현대 사람들이 가장 많이 사용하는 토픽모델이 바로 LDA입니다.
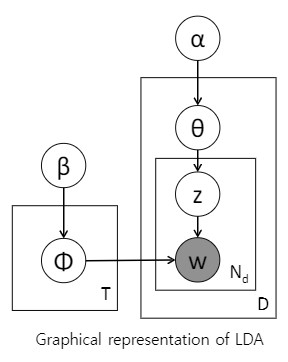
LDA라는 모델의 구조의 Graphical representation이 아래 그림입니다.
Neural Network나 Bayesian Network랑 똑같이 이해해주시면 됩니다. 노드가 있고 간선이 있고요.
하지만 베이즈 네트워크에서 보지 못했던 그림이 있어요.
바로 노드의 색이 다르다는 것과 네모박스가 있다는 것입니다.
네모박스는 반복을 말합니다.
바깥쪽 큰 네모 박스에 D라고 써있는데 이는 Document의 개수를 말합니다.
네모박스가 반복이라고 이야기했잖아요?
도큐먼트 개수만큼 있어!라는 뜻입니다.
바꿔말하면 저 θ(세타)가 도큐먼트 개수만큼 있는 것입니다.
가령 1번 문서와 2번 문서가 있을 때 1번문서를 위한 세타가 있고 2번문서를 위한 세타가 또 따로 있는 것입니다.
이 세타라는 애는 문서 d의 topic distributior입니다. 토픽의 분포에요.
예를 들어 문서 1이 정치 이야기 60%, 농구 이야기 40%가 있었다하면 문서 1에 대한 세타는 6:4 분포로서 또는 더해서 1이 되도록 0.6:0.4 이런식으로 표현되게 됩니다.
D 박스 안에 Nd라는 박스가 하나 더 들어가네요?
N이라는 것은 단어의 개수입니다.
하나의 문서를 단어 W들의 모음이라고 보는 것입니다.
그런데 Z라는 노드를 거쳐서 오게 되는데 이것은 이따 예제를 통해 설명하겠습니다.
단어 W는 문서마다 N개 존재한다해서 Nd라고 표현한 것입니다.
그리고 W는 실제로 드러나는 데이터이기때문에 색칠이 되어있는 것입니다.
바꿔말하면 우리한테 주어진 관측은 바로 단어의 나열입니다.
사람 눈에 보이는게 저거 밖에 없는 것입니다.
색깔이 없는 상태의 노드들은 즉 데이터가 아니고 보이지 않는 것이고요.
알파부터 베타까지 보면 전부 화살표가 아래를 향하고 있죠?
이러한 구조에서 드러나는 것이 가설 그자체에요.
이러한 단계를 통해서 문서를 작성했을거야 하고요.
다른 예로는 저 자동차는 내부적으로 이렇게 이렇게 생겼을거야 하고 미루어 짐작하는거에요. 실제로 자동차 내부를 본적도 없으면서 외관만 보고 가정해가는 것이지요.
그러다보니 사람마다 다르게 생각할 수 있겠죠?
다른 구조를 가진 모델로 설계를 할 수도 있는 거에요.
다른 아이디어나 관점에 의해서 설계를 하게 되는 것입니다.
그런데 그 데이터나 특성에 잘 맞아떨어졌다면 훌륭하죠.
바로 예제를 봅시다.
지금부터 볼 예제는 인공지능 책을 분석을 완료되어있는 상태에서 문서를 생성한다는 가정을 합니다.
처음에는 원래 문서들에 색깔이 없는 상태로 분석해갈거잖아요?
그런데 이 예제를 볼때 관점은 이미 학습이 다 되어있다고 가정하고, 이러이러한 과정에 의해서 단어들이 쓰여졌을 거야. 라는 가설을 가지고 시작하게 됩니다.
그 안에 있는 단어들을 가지고 문서를 생성해나가는 과정으로 바꿔서 보는 것 입니다.
α(알파)나, 세타나 이런게 다있다고 가정하고 시뮬레이션하는 거라고 생각해주세요.
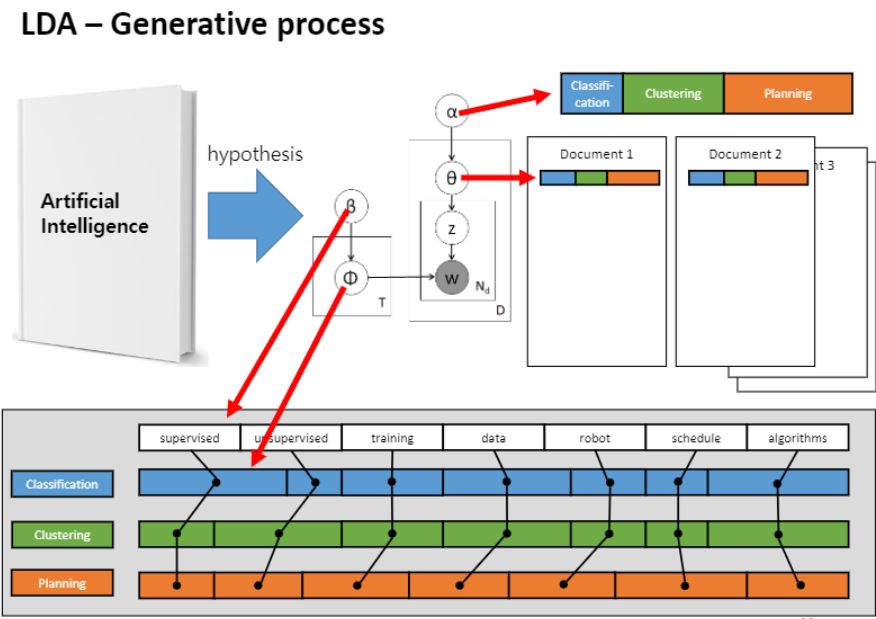
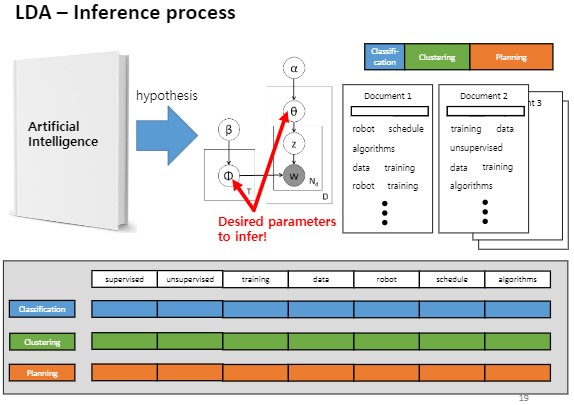
상단 막대기 Classifiactin, clustering, planning이라는 카테고리로 그림과 같이 나뉘어져있다는 Prior(사전지식)이 주어집니다.
1번 토픽은 classification, 2번 토픽은 clustering, 3번은 planning 총 세가지 토픽이 있다고 가정하고
막대 바 길이가 긴 녀석들일수록 비중이 더 많은애들이에요.
이것을 사전지식으로 사람이 주는것입니다.
그 다음 문서마다 세타가 존재한다고 했었죠.
그래서 문서1에 해당하는 비율이 색칠된 상태로 주어져있고, 문서2에 대한 토픽 비율도 주어져있습니다.
왼쪽엔 β(베타)가 있는데 vocabulary라고 부르는데 이 단어가 얼마나 나타나는지를 보여주는 단어들에 대한 사전 지식입니다. 그런데 여기서는 모든 단어가 다 똑같은 비율로 있다고 가정하는거에요.
똑같은 비율인지는 어디에 드러나냐면 supervise, unsupervised,…,algorithms 여기 흰색 막대기 부분이요.
Φ(피)는 토픽 자체인데 이것의 실체는 바로 supervised는 얼마만큼 등장할 것같고, 어떤 단어는 비교적 덜 등장할 것같고.. 그러한 단어들이 등장할 확률을 비율로서 표현한 것이 토픽의 실체입니다.
그리고 이러한 피는 토픽마다 존재합니다.
supervised를 위한 단어 분포가 있고, clustering을 위한 단어 분포가 있고, planning에 대한 단어 분포가 각각 따로따로 있는 것이죠.
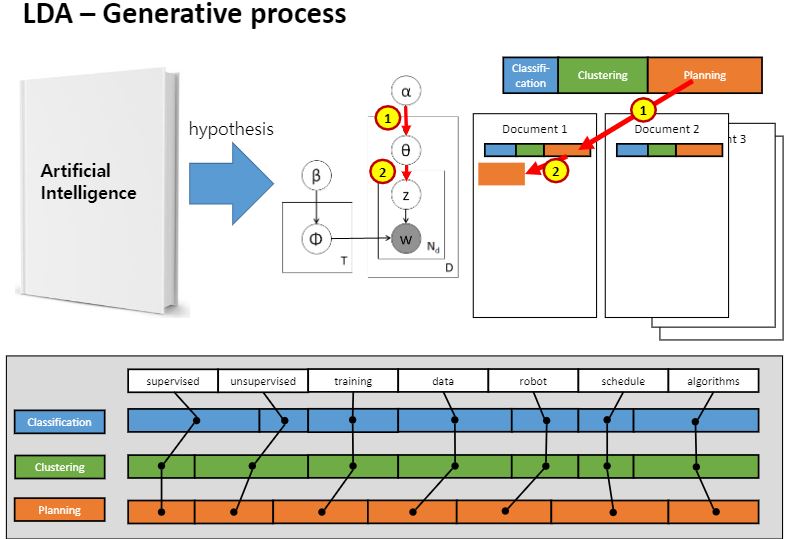
사전지식으로 주어진 분포 알파를 기반으로 첫번째 도큐먼트에 대한 세타를 샘플링합니다. 분포 알파를 기반으로 분포 세타를 샘플링하는거에요.
저게 어떻게 뽑힌거냐면..
이거 아시나요? 이것처럼 뽑혔다고 생각하시면 됩니다.
ㅎㅎ모르시는분 여기 링크 참고하세요.
https://www.youtube.com/watch?v=PS17oO57cts
당연히 그럼 칸이 넓은애가 걸릴 확률이 높겠죠?
어쨌든 그렇게 나온 단어가 바로 Z입니다.
세타 분포에서 걸려나온 문서1의 첫번째 단어가 주황색 토픽이라는 것을 Z로서 얻어온거에요.
첫번째 단어에 대한 토픽은 결정되었어요.
토픽만 결정된 거지 단어가 결정된 것은 아니기 때문에 한 번 더 베타를 또 멈춰!해서 뽑아와야해요.
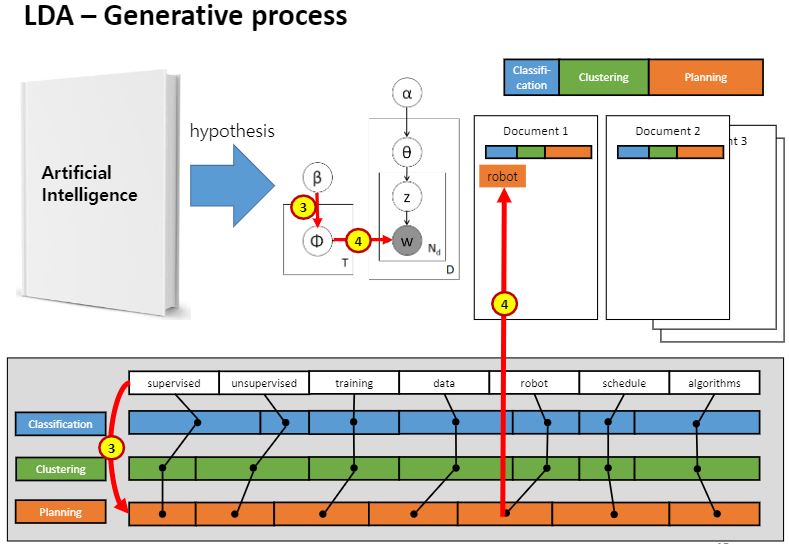
지금 사람이 문서를 쓰는 행위에 대한 가설을 세워서 거꾸로 가고 있다는 걸 잊지마세요.
그 가설이 세타로 표현이 된거에요.
그렇게 걸린 단어가 robot이라고 합시다.
사람이 글을 쓸 때 토픽을 먼저 결정짓고 그 토픽에 대한 단어는 뭐로 해야지!하는 흐름을 고려하는 것입니다.
처음에 세타라는 전체 사전지식으로부터 분포가 만들어졌고, 샘플링해서 토픽이 결정되었어요.
또 샘플링해서 단어가 결정되었어요.
그렇게 가설을 세운거고 그 내용을 시뮬레이션하고 있는 것입니다.
모든 도큐먼트에 대해서 이 과정이 반복되었다고 합시다.
크게 어려운 내용은 아닌 것 같죠?
그런데 이를 어렵게 만드는 점은 뭐냐면,
이 모델은 Unsupervised learning에의해서 학습되는것이기 때문에 아래와 같은 Document 분포에 대한 사전지식 없음 상태라는 것이지요.
우리가 실제로 토픽모델을 쓸 때는 거꾸로 오직 단어만 다 있는 상태에서 세타가 몇일까, 피에 해당하는 토픽에 해당하는 단어의 비율이 뭔가?를 얻어내려고 하니까 어려운거에요.
그래서 이런 작업을 하기 위해서 수학적 지식이 아주 많이 필요합니다.
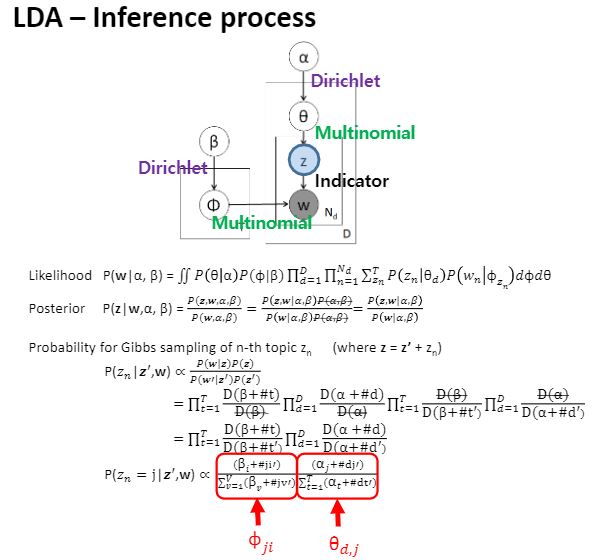
LDA 모델에서 저 화살표 하나 하나는 그냥 나오는 것이 아니라 사실 어떤 probability distribution을 의미합니다.
베타에서 피로 가는 경우와 알파에서 세타로 가는 경우에는 dirichlet이라는 분포를 따르고 있고,
세타에서 z로 가는 것과 피에서 w로 가는 것도 멀티노미얼,
z라는애는 스탑해서 결정된 토픽 자체였자나여?
걔가 결정되었을 때 비로소 우리는 왼쪽에 있는 피중에서 특정한 토픽을 선택한 것이기 때문에 그래서 가리키는 용도다 라는 의미에서 indicator라고 부릅니다.
이러한 분포에 의해서 모델이 설계가 되어있습니다.
Likelihood와 Posterior에 대한 수식이 확인되고 있고요.
나중에 학습을 할 때는 한 번에 하는 것이 불가능해서 gibbs sampling이라는 알고리즘을 통해 파라미터 estimation 및 학습하게 됩니다.
학습 이후에는 하단 가장 마지막 부분 수식에서 보는 바와 같이 z에 대한 probability를 구하기 위해 전개했더니 왼쪽 term은 피, 오른쪽 term은 세타만 남는다라는 것을 알 수 있습니다.
수식은 참고만 해두셔도 좋을 것 같습니다.
토픽모델 대표모델로서 LDA모델을 봤는데, 단어들만 잔뜩 주어진 상태에서 토픽들의 분포인 세타를 얻어지게 해주고, 동시에 토픽의 실체인 단어에 대한 분포도 얻게 해줍니다.
예제에서 classification이라는 토픽도 사실 사람이 붙인 거에요.
사실은 처음에는 단어들의 나열만 있을 뿐이에요.
사람이 학습 시작 직전에 몇 개의 토픽이 있는지 개수만 말해줄 뿐입니다.
그럼 LDA는 단순히 이 수식에 기반해서 워드 디스트리뷰션을 업데이트해나가는 것일 뿐이에요.
나중에 학습이 끝나고나면 사람이 첫번째꺼에서는 supervised가 많이 나오고 뭐가 많이나오는 것을 보고서 얘는 classification이라고 레이블을 붙혀주는 것입니다.
한계점이죠. 결국은 사람이 해석해야한다는 것
베이지안 네트워크를 통해 데이터가 생성되는 그 과정을 보여준 것이기 때문에 복잡하다고 생각하실 수 있어요.
LDA라는 모델은 최초 probability 모델은 아니에요.
하지만 가장 많이 사용되는데, graphic에서 드러나듯 그럭저럭 괜찮게 잘 설계를 했기 때문입니다.
예를들어 외관만을 보고 있다하고, 아직 자동차가 없다고 생각하고 이렇게이렇게 하다보면 바퀴가 돌아가는 걸껄?
이런 가정을 하는거거든요?
마찬가지로 지금 이런 단어들이 없다고 가정을 하고 한장한장 써가는 살펴볼거에요.
처음에는 알파에서 토픽 분포를 가정하고, 베타에서 단어들의 분포를 가정하고, 그러한 분포로 부터 문서마다 존재하는 세타를 가정하고
피는 각 토픽마다 존재할 것인데, 서로 다른 토픽이니까 당연히 토픽마다 분포가 다르겠지요.
서로다른 분포가 있을거고 이게 이미 존재한다고 이미학습이 다 되어있다고 가정하는거에요.
하지만 실제로는 도큐머트에 대한 세타와 파이값은 다 없고 uniform합니다.
서로가 똑같은 분포를 가진상태로 시작한거에요.
오로지 단어만 가지고 세타와 피들을 찾아가는 겁니다. 그래서 이게 널리 사용되는겁니다.
여기서 하나 재밌는 걸 짚고 넘어갈 건데요,도대체 단어들만 주어졌을 텐데 어떻게 세타와 피를 구해나가는 것일까요?
Z가 바로 그 역할을 하게 합니다.
왜 단어마다 굳이 토픽을 설정하게 하는걸까에 핵심이 있습니다.
Random variable로서 w라고 되어있는 단어들만 가지고 있는 상태에서 세타와 피를 찾아가게 하는 아주 중요한 개념이 Z입니다.
그래서 z가 단어마다 존재하도록 가정한 것이구요.
각 단어마다 무슨토픽인지를 맞추게되는것이면 즉 Z를 맞추면 다 된거에요.
세타는 문서에 대한 토픽의 분포죠.
문서1에 대한 세타가 아직 구해지지 않았아요.
그런데 각 단어마다 서로 다른 색으로 칠해놓고 문서내 토픽들을 취합하여 그 분포를 볼 수 있다면 이 문제는 끝난 거 잖아요?
각 단어마다 매겨지는 토픽을 각각 세서 분수로 만들어주면 그게 토픽 분포가 되는거죠.
또한 해당 토픽에서 더 많이 나타난 단어들에 가중치를 더 크게 둘 수도 있는거지요.
그러다보니 z라는 애만 구하면 세타와 피는 자동으로 구해집니다.
Doument1에서 나온 단어들간의 순서는 중요하지 않습니다.
단어들간 서로의 상대적인 위치를 전혀 고려하지 않기 때문에 Bag of words, BoW 단어의 가방이라고 말할 수 있습니다.
LDA는 복합 도규먼트를 백오프워드로 취급합니다.
다음 글에서는 LDA에도 사용될 수 있는 estimation 방법인 EM algorithm에 대해 기술하겠습니다.
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!