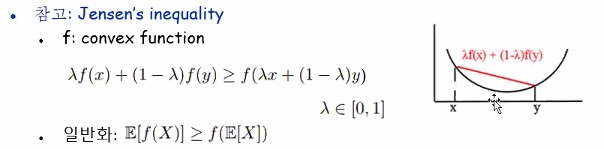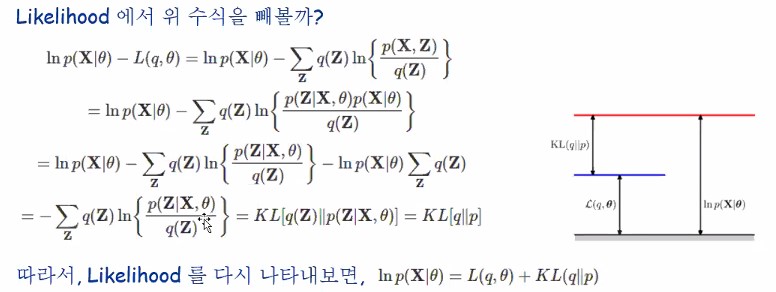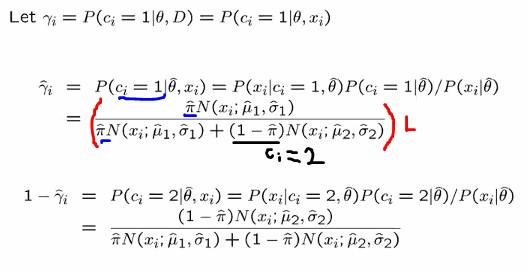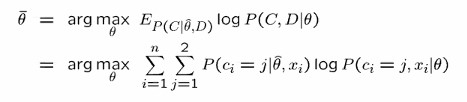Expectation Maximization_Machine Learning(16)
Intro
학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.
기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.
gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.
이번 시간에는 파라메터 estimation method인 EM algorithm을 배웁니다.
EM(Expectation Maximization)
Expectation Maximization을 직독직해하면 기대값을 최대화해주는 알고리즘입니다.
기계학습의 본질은 임의의 모델의 파라미터를 데이터로부터 학습하는 것입니다.
그렇다면 무엇의 기대치를 최대화하려는 알고리즘일까요?
EM 알고리즘은 unsupervised learning 모델을 학습하는 것입니다.
EM을 설명하면서 동시에 gMM을 설명할 거에요.
GMM은 클러스터링에 쓰이는 기술입니다.
GMM을 학습시킬 수 있는 알고리즘이 EM 알고리즘입니다.
이거 배우다보면 이전 시간에 다뤘던 토픽모델 LDA에서 z를 구하면 나머지를 구하게 되는 것과 비슷한 내용을 볼 수 있게 됩니다.
EM 알고리즘의 간단한 예제로 영화추천을 가정하고 예제를 살펴봅시다.
영화가 만족스러웠으면 1 아니면 0으로 표기한다고 합시다.
K가 영화의 총 개수입니다.
홍길동이라는 사용자가 1,2,3번 영화를 보고나서 각각 101점을 줬습니다.
남은 두가지 영화들은 어떻게 평가를 할지에 대한 확률값을 계산하여 추천을 하게 될 겁니다.
a~e는 각각 1또는 0 값을 갖게됩니다.
E-step에서는 파이값을 이용하여 conditional probability를 계산하게 됩니다.
M-step에서는 Joint probability를 이용해 파이값을 업데이트하게 됩니다.
이렇게 E-step과 M-step을 계속 반복하면, 수렴(coverage) 상태에 다다르게 됩니다.
그래서 이것도 iterative에요.
이 예제에서의 EM 알고리즘의 목표는 결국 최종 파이를 계산하여 얻는 것을 말합니다.
Expectation Maximization Algorithm도 Likelihood를 최대화시키는 파라메터 찾기가 목적입니다.
그래서 MLE랑 알고리즘이랑 같아보일 수 있습니다.
하지만 MLE는 최적 파라메터를 직접 계산한다면, EMdms E-step, M-step을 반복(iterative process)하여 파라메터를 점차적으로 최적화하게 된다는 점에서 다릅니다.
MLE로 직접 계산하기 어려운 경우에 사용되게 됩니다.
예를 들면 미분 불가하다거나, 모델이 복잡한 경우(ex:mixture model) 즉 convex형태가 아닌 경우에 해당합니다.
우리가 EM 알고리즘으로 풀려는 것들은 대부분 global optima를 찾기 어려울 때 입니다.
Convex 형태가 아닐 경우가 그에 해당하겠지요.
물론 convex 형태에도 EM 알고리즘을 쓸 수는 있어요.
굳이 그럴 필요가 없을 뿐이에요.
수학 개념 중 Jensen’s inequality라는 것이 있어요.
고등학교 미적분학에서 배웠던 것 같아요.
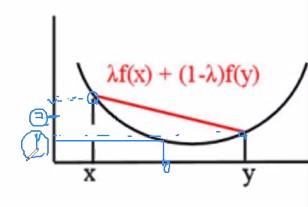
1은 x와 y 중간값이라고 합시다. 2는 f(x)와 f(y)의 중간값이라고 할 수 있어요.
2는 1보다 항상 같거나 크다라는 말을 하는 거에요.
왜냐하면 함수 f가 convex 형태이기 때문입니다.
E는 expectation을 의미합니다.
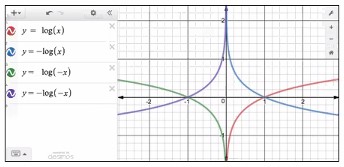
위로 볼록한 concave 형태의 함수는 부등호 방향이 반대로 되겠지요?
대표적인 그러한 함수가 바로 log function 입니다.
왜 EM 알고리즘을 이야기하다가 위 수식을 이야기하게되었을까요?
우리가 구하고자하는 파라메터를 세타라고 둡시다.
그리고 파라메터 세타로부터 생성된 최적의 값을 z라고 해요.
이러한 z를 데이터로부터 계산해나갑니다. 그러면 z를 얻게 되면 세타를 궁극적으로 얻을 수 있게된다는 것이죠.
토픽모델링 LDA에서도 마찬가지에요.
Likelihood가 뜻하는 것이 얼마나 데이터가 그럼직한가 였잖아요?
아래와 같이 데이터 X에 대한 likelihood를 모노함수 log 를 씌워 표현해줍니다.
한 문장이 생성될 때 토픽 1번에 의해서 생성될수도 있고 2번에 의해서 생성될수도 있고 모든 단어들에 의해 생성될 수 있는 거잖아요?
그러한 전체 경우의 수가 분모가 됩니다.
그게 p(X,Z|세타)에서 조건인 세타 부분을 말하고 있는 거에요.
그리고 분포 함수를 또다시 말해요.
토픽모델 LDA에서도 나왔던 내용이에요.
Z가 단어마다 샘플링되었었잖아요?
여러 개 중에 스탑 해서 고른게 z라고 말했던 것 기억나시죠?
단어별로 막대길이 다르게해서 그렸던 이유는 사전지식이라고 했었는데 일단은 그러한 분포가 있어야할 것입니다.
그게 바로 여기서는 q에 해당합니다.
그 다음 수식에서 젠슨스 인이퀄러티가 나오네요.
부등호 기준 우변을 L이라고 둡시다.
좌변은 log likelihood죠?
kL divergence 죠!
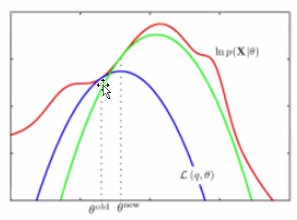
저 오른쪽 그림에서
Log likelihood가 높이가 높을수록 좋은거라고 합시다.
그리고 L함수가 젠슨스에 의해서 log함수가 concave니까 더 작겠지요.
그럼 그 차이를 보는 것이 KL divergence에 해당한다는 걸 말씀드리는 겁니다.
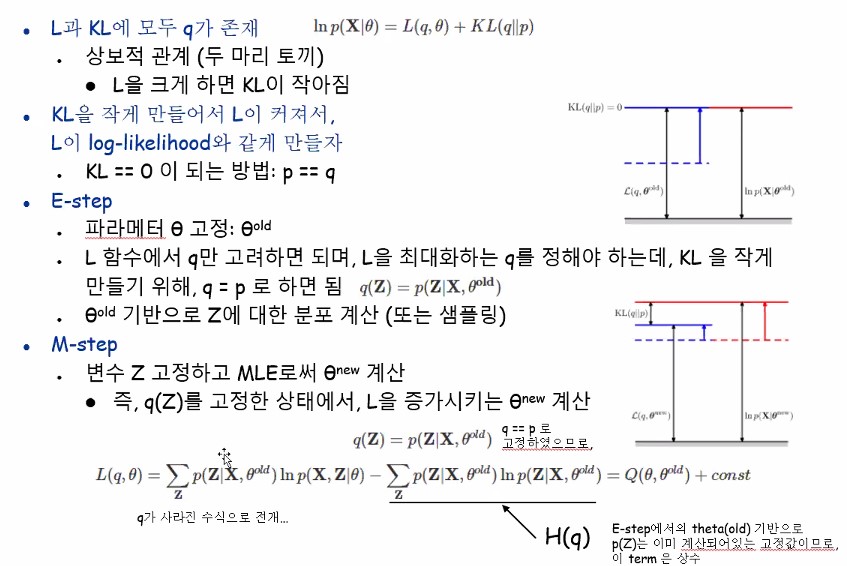
L과 KL에는 모두 q가 존재하고 L이 클수록 KL은 작아지고 L이 작아질수록 KL은 커집니다.
이 두마리토끼를 동시에 절대 잡을 수 없고 우리는 KL을 작게 만들어서 L을 키우고 싶은겁니다.
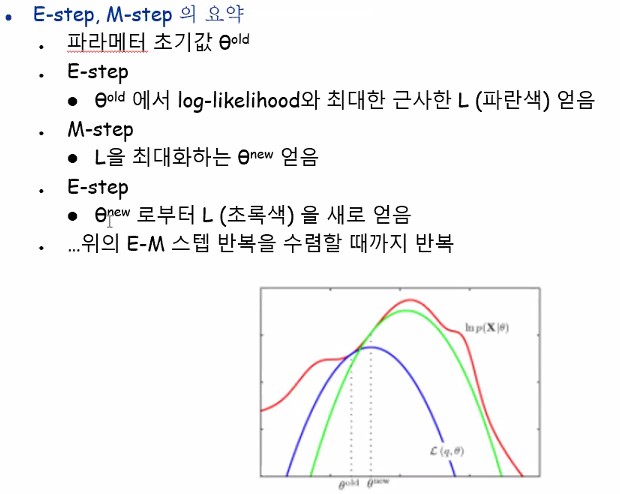
잠시 원활한 이해를 위해 이부분을 건너뛰고 E-step과 M-step의 요약을 먼저 봅시다.
저 빨간 꾸불꾸불한선이 가장우리가 얻고싶은 likelihood라고 합시다.
그리고 현재 우리는 파란선 상태라고 합시다.
세타 올드는 접점을 말하고 세타 뉴는 파란 컨케이브함수의 최대값이고요.
근데 가장 높은 부분에 해당하는 초록색(사실 더 갈수있음)까지 서서히 움직이면서 세타뉴를 갱신해가겠지요.
돌아와서.. KL함수를 그래서 0으로 만들어주는 애를 찾을거에요.
거리가 가장 작아지도록이요.
그러려면 분모분자가 같아지면 됩니다.
그럼 1이되잖아요? 그럼 로그함수에 의해서 0이 될 거니까요!
그래서 p==q라고 써놓은 거에요.
E-step에서 우리는 파라메터 세타를 고정시킵니다. 세타 old로요
우리는 세타 old를 기반으로 q를 구했습니다.
잘 이해하기 위해서 LDA에서의 예시를 봅시다.
세타는 토픽 분포입니다.
막대기처럼 생겼어요.
스탑해서 a는 카테고리 2번! 하고 골랐어요.
그래서 워드 분포 2에다가 a를 썼어요.
확률 분포자체를 계산해낼 수도 있긴한데 어쩄든 보통 샘플링해서 단어 빈도 계산해서 과정자체가 Estep이에요.
위 예제에서는 방금 말한 과정 전체가 Estep입니다.
그러케 단어 네개에 대해서 2,1,3,1이렇게 매겼다고하면은 그게 estep 끝난 겁니다.
Mstep은 분포보고 막대기 다시 그리는 과정에 해당합니다.
EM algorithm에서는 이를 “Mstep에서는 변수 Z고정하고 MLE로써 세타 new를 계산한다”라고 표현합니다.
처음에는 파라메터를 가정하고 estep, 그 다음엔 파라메터를 갱신하는 mstep
왼발(파라메터)을 고정하고 오른발(z)를 내밀고 이번엔 z를 고정하고 왼발을 내밀죠.
그걸 한번의 iteration이라고 합니다.
계속 반복해요. 특정 임계치가 될때까지요.
왼쪽이 분자부분, 오른쪽이 분모부분인데 오른쪽이 자세히보면 엔트로피거든요?
q(z)=p(z)라고 가정했기 때문에 estep을 통해서 이미 정해져있어요.
그래서 그냥 이 부분은 상수값입니다.
왼쪽 텀 같은 경우에는 우리가 구하고자하는 세타 new에 해당하는 항이 있습니다.
그래서 반복하기 위해서 왼쪽항을 다시 q라는 함수로 표현한거고 오른쪽은 상수constant라고 표현한거에요.
GMM(Gaussian Mixture Model)
GMM은 모델이고 EM은 학습할 수 있는 알고리즘이에요.
GMM(Gaussian Mixture Model)은 클러스터링 등에서 사용되곤하는 모델중 하나입니다.
이를 이해하기 위한 상황은 아래와 같이 가정합니다.
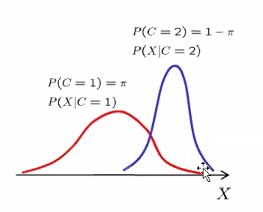
우리에게 Bi-modal dataset이 주어졌습니다.
한 개의 Gaussian 으로는 모델링이 불가능한 경우요.
가우시안 모델 두개로부터 가정해야하는 상황이라고 합시다.
클러스터링은 특히 더 그래요.
데이터 특징을 잘 관찰하고 탐색적으로 데이터를 분석해보고 클러스터를 n개로 정하고 그런거지요.
이 경우에서는 클러스터 개수가 최적이 2개인 경우를 가정하자는 거에요.
태스크는 데이터가 가진 특징을 보고 어느 가우시안에 해당하는 지를 골라줘야 하는거에요.
어느 가우시안인지에 대한 확률 변수로 C라는 변수를 정할거고요. 이게 앞서 EM 알고리즘에서 말했던 Z에 해당하는 것입니다.
C는 Bernoulli random variable로 두 모델 중 어느 Gaussian인지를 나타내게 됩니다.
LDA로 비유하자면 어떤 토픽을 가리키는지가 Z였잖아요?
여기서는 어느 가우시안인지 가리키는 용도인 겁니다.
빨간색 가우시안을 나타내는 확률을 파이라고 하면 바이 모달이니까 파란색 가우시안의 확률이 1-파이가 되겠지요.
| 1번가우시안에 의해서 데이터x가 생성되었을 확률이 P(X | C=1)입니다. |
| 데이터 x가 가우시안 2번에 속할 확률이 얼마나 되니? 이게 P(X | C=2)입니다. |
가우시안 1에 의해서 x가 생성된 x값이 얼마나 likely 하니…라는 뜻이지요.
C가 1일 때 이 가우시안에 의해서 x가 얼마나 그럼직한가에 대한 높이값이 그 확률 값이에요.
그래서 가우시안 랜덤변수 역할을 하는 것은 데이터 X입니다.
그럼 모델 파라미터를 다 정리해보면 파이, 뮤1, 시그마1, 뮤2, 시그마2 다섯개지요?
Prior는 가우시안1과 2 중에 어느쪽이 더 대세니를 말하는 거에요.
그 정보가 P(c=1)에 들어갈거에요.
데이터 x가 있는데 그게 1번 가우시안에서 얼마나 likely하니가
P(C=1)P(X=x|세타, C=1)입니다.
1번 가우시안에 해당하는게 저거고 오른쪽항은 2번 가우시안에 해당하는거고 두개를 더한다는 것이 전체 확률이 되겠습니다.
| 아래수식은 왼쪽에 P(C=1)이 파이가 되었구 P(X=x | 세타,C=1)이 N()으로 바뀐거고요 |
LDA 학습시키기위한 알고리즘은 여러가지가 있구 그중 딱하나 EM 소개시켜준 것 입니다.
그래서 결부시켜서 설명하는거에요!
전체 데이터를 D라고 치환했어요.
전체 데이터에 대한 라이클리후드에 log를 붙이면 더하기로 풀어서 쓸 수 있지요.
이 식은 자세히 보니 앞서 우리가 정의했던 식 그대로네요.
cj는 j번째 데이터가 가진 C값을 말합니다.
c값이 가우시안 1인 데이터의 개수를 의미하는 것이 n1, c값이 가우시안 2인 데이터들의 개수가 n2입니다.
동그라미하나하나가 데이터에요.
C를 우리가 알고있다는 가정하에 우리가 이렇게 구할 수 있는거에요.
전체 데이터 n개중에서 1 그게 파이겠지요?
위 식을 보면 c값을 알고나니까 모든 파라미터가 다 구해진다는 것을 알 수 있습니다.
근데 문제는 c를 모른다는 거지요.
Soft clustering이라고해서 1번에 속할 확률값, 2번에 속할 확률값을 표현하기도 하지만
어쨌든 C를 모른다는 겁니다 현재는
그래서 EM알고리즘을 씁니다.
종료 조건은 엔지니어가 주기 나름입니다.
우리가 배웠던 것에 의하면 q==p라고 가정함으로써 C를 가지고 감마를 구하고 감마를 가지고 C를 구합니다.
i번째 데이터가 1번 가우시안일 확률을 감마i로 표현하고있습니다.
감마라는 건 probability로 이야기하고 있습니다만 probability를 갖고 있다하면 sampling을 할 수도 있는거에요!
감마를 어쨌든 구해놓고 그 감마를 사용해서 mstep에서는 세타 new를 구하게 됩니다.
E라고 되어있는건 expectation을 말하며 세타,D 부분은 확률 분포를 말합니다.
그거를 사용해서 C와 D에 대한 joint probability를 구해서 expectation을 최대화 시키는 세타를 구해라 라는 수식이 3번에 해당합니다.
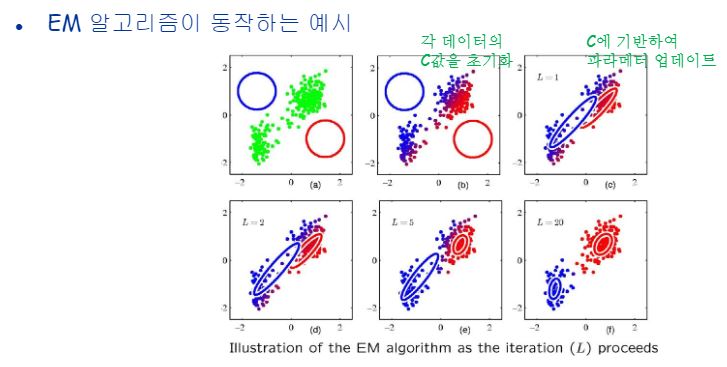
두 개의 가우시안이 mixture 되어있는 상황에서 군집화를 보여주는 그림입니다.
개념적으로 본거고 진짜 수식으로도 확인해봅시다.
EM은 Uniform distribution으로 초기 파라메터 세타를 주고 Estep, Mstep을 거쳐서 반복하며 optimal한 세타값을 구해갑니다.
예를 들어 떡볶이를 친구들하고 먹었어요 3000원이 나왔는데 n빵하는 상황을 uniform distribution이라고 합니다.
균등하게! 그게 uniform distribution입니다.
EM 알고리즘은 global optimal을 구하게 된다는 보장은 없습니다.
Local optimum을 얻게되는 것이죠.
그러다보니 초기값 영향을 크게 받습니다.
뮤값들 두개를 무작위로 선택하여 초기화할 수도 있고
그로부터 시그마값들은 초기화를 시킬 수 있겠죠?
그리고 파이를 0.5로 둠으로써 Estep에 진입합니다.
Estep에서는 새로운 감마i를 구할거에요. 감마i는 세타가 고정된 상황에서의 Z값 계산으로 조건부 확률에 의해 계산이 이루어집니다.
베이즈 이론에 의해 도출된 식전체는 Likelihood를 말합니다. 파란색은 Ci=1 인 경우에 해당하며 검정색은 Ci=2인 경우에 해당합니다.
분자에서 파이는 Gaussian 1일 자체 확률을 말하며 뒷부분은 얼마나 그럼직한지를 normal distribution에 의해 표현하고 있는거지요.
이렇게 감마에 대해 구해서 Estep이 끝났습니다.
i번째 감마를 구하긴했지만 n개의 데이터가 있으면 n개의 감마가 나오게됩니다.
사용되는 파라메터들 5개가 모두 사용되지요.
이미 주어져있다고 가정하는거에요. 우리가 초기값을 줬으니까요!
특히 세타를 고정시키고 감마를 구했어요
Mstep에서는 이 세타를 구하게됩니다.
Estep에서 구한 감마를 고정시키고 세타를 구합니다.
알고리즘의 이름처럼 기대값을 최대화시키는 세타를 구한다는 것을 알 수 있습니다.
지금 파라메터 세타 안에 다섯개가 들어있잖아요?
그 중 뮤 1을 구하는 과정을 먼저 봅니다
=0로 두고 미분해서 구하고 있습니다.
감마의 값이 실수가 아니라 0또는 1이라고 생각해봅시다.
저 수식은 1번클러스터에 해당하는 애들만 다 더하라는 말을 하고 있습니다.
Weight를 크게해서 더하므로(Weighted sum) 그게 평균이 되는거에요.
M1에 대해서 argmax하잖아요?
세타 전개 두번째줄수식보면 일반화해서 쓴거고, 그걸 구체적으로 뮤원에 대해쓴게 for 뮤1 바로 밑줄식이에요
미분해서 0으로 놓고 전개하면 저식이 나옵니다.
그렇게 비슷한방법으로 다섯개의 파라미터들을 다 구하고 다시 estep으로 가서 감마를 갱신시킵니다.
한걸음씩 가다가 특정 종료조건에 다다르면 학습을 그만하는거지요.
의외로 GMM이 음성인식에서 많이 사용됩니다!
정리하며,,,
EM이 어떻게 convex나 concave가 아닌 형태의 세타도 최적화할 수 있다는 걸까요?
문제가 ANN에서 역전파랑 똑같습니다.
최적화할 대상에 대한 함수를 그려보는데, 시각화해서 보여주면 편하니까 2차원으로 많이들 표현하죠.
특정 합수값이 최소가 될 수 있게 하는 세타를 구하는건 이해가 되실겁니다.
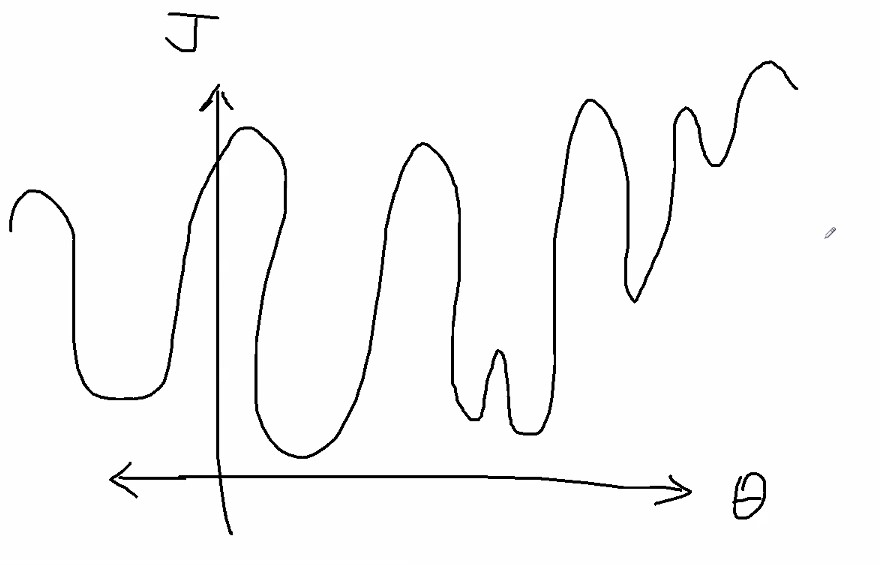
근데 만약 미분가능은한데 엄청 꾸불꾸불하게 아래처럼 생겼다고 합시다.
어떻게 최적값을 구할 수 있겠습니까
근데 실제로 만나게되는 데이터들은 저런식으로 나온다는 것이죠.
노이즈도 있고 에러도있고요..
그러한 노이즈에 대한 영향은 최대한 덜 받으면서 최적화해야할 대상에 대한 함수가 저렇게 생겼다고 하면
최소화/최대화 시켜주는 세타를 찾을 수 있느냐하는 문제에서
Global optima는 보장할 수는 없습니다.
보통은 우리가 이런 최적 값을 구할 때 편미분=0을 두고 구하곤 하자잖아요?
근데 이렇게 고차원의 비선형 함수는 미분이 너무 어려워서 못 구해요.
이러한 이유로 인해 글로벌옵티마도 못구하는것입니다.
그래서 차선책이 뭐냐하면, 임의의 세타를 가정해놓고
거기서 접선기울기 따라서 그라디언트디센트구요.
그게 체인룰에 의해서 백프로파게이션 알고리즘을 거쳐서 가중치들을 갱신시키며 점점 더 낮은곳으로가다가 그 지역에서의 최소인 지점의 세타를 찾는겁니다.
그렇게 로컬이더라도 옵티마를 구할 수 있는것이구요.
미분=0 이 방법으로 구할 수 있던 문제가 아니라는거에요.
EM도 똑같습니다.
엄청 꾸불꾸불해서 미분이 너무 어렵거나 =0으로 구할 수가 없는거지요.
그래서 Z랑 세타를 가지고 한스텝씩 로컬 옵티마에 다가가는 것입니다.
개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!