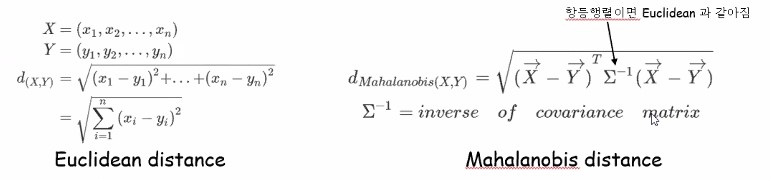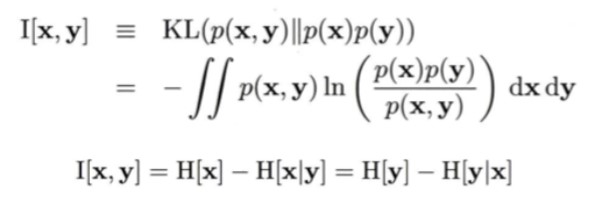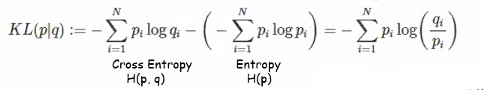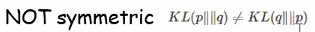Kmeans Clustering & Knn & Hierarchical Clustering_Machine Learning(12)

Intro

학교 수강과목에서 학습한 내용을 복습하는 용도의 포스트입니다.
그래서 이 글은 순천향대학교 빅데이터공학과 소속 정영섭 교수님의 “머신러닝” 과목 강의를 기반으로 포스팅합니다.

기존에 수강했던 인공지능과목을 통해서나 혼자 공부했던 내용이 있지만 거기에 머신러닝 수업을 들어서 보충하고 싶어서 수강하게 되었습니다.

gitlab과 putty를 이용하여 교내 서버 호스트에 접속하여 실습하는 내용도 함께 기록하려고 합니다.

• 원격 실습환경구축 따라하기
  

• Machine Learning(1) 포스트 보러가기
  

• Machine Learning(2) 포스트 보러가기
  

• Machine Learning(3) 포스트 보러가기
  

• Machine Learning(4) 포스트 보러가기
  

• Machine Learning(5) 포스트 보러가기
  

• Machine Learning(6) 포스트 보러가기
  

• Machine Learning(7) 포스트 보러가기
  

• Machine Learning(8) 포스트 보러가기
  

• Machine Learning(9) 포스트 보러가기
  

• Machine Learning(10) 포스트 보러가기
  

• Machine Learning(11) 포스트 보러가기
  

• Machine Learning(13) 포스트 보러가기
  

이번 시간에는 Kmeans, Knn, Hierarchical Clustering을 배웁니다.

Semi supervised learning

Semi supervised learning은 Unsupervised learing과 supervised learning의 중간이겠지요.

데이터가 너무 적은 경우 또는 불균형 데이터를 갖는 경우 데이터가 너무 적은 경우에는 어떻게 하는 것이 좋을까요?

첫 번째로. transfer learning(전이학습)을 통해 해결할 수 있어요.

학습 데이터가 부족한 분야의 모델 구축을 위해 유사한 데이터가 풍부한 분야에서 훈련된 모델을 재사용합니다.
(ex: pre-trained model의 파라메터로 초기화하는 것 등)

한글->중국어 데이터가 100개만 있다고 할 때, 걍 100개만가지구 학습시킨것보다 훨씬 나은 성능을 보입니다.

두 번째로, Distant supervision 가 있습니다.

약하게 레이블링된 트레이닝셋을 이용합니다.
훈련데이터는 휴리스틱이나 규칙에 기반하여 자동적으로 레이블되어있는 것이지요.

데이터 불균형시 또 다른 방법으로는 소개했 듯이 up/down sampling 이 있구요.

GAN을 이용하여 fake data를 생성하여 robustness를 높이기도 합니다.

두번째 방법은 loss weight control인데요.

Cost sensitive learning이란 학습 데이터의 label 비율에 비례하게 loss 함수에 weight 조절을 함으로써, 비교적 적은 비율의 Label에 해당하는 데이터에 더욱 민감하게 학습하는 것을 말합니다.

Focal loss 는 학습 데이터 label 비율이 높아서 상대적으로 쉽게 분류가 가능한 Label에 대한 weight를 작게 조절함으로써, Label 비율이 작은 데이터들에 집중하도록 조절하는 것을 말합니다.

Q. 둘 다 같은 거 아니에요?
Cost-는 레이블 비율에 의해서만이죠,

focal은 쉽게 분류가 가능한 데이터가 판별이 될거잖아요?

실제로 모델을 돌려보면요?
성능 차이가 나는 여러 이유들중에 하나가 레이블 비율이 될수 있는 것 뿐이고요.
쉽게 분류가 안되는 데이터들에 대해 더 weight를 크게 조절하겠다 라는 것을 말합니다.

이런 방식은 부스팅에서도 봤었죠.

Semi supervise learning

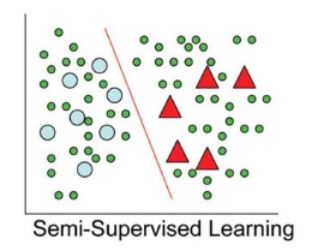
예제는 동그라미와 세모 두가지 클래스에 대해 분류하는 바이너리 분류기입니다.

그림에서 보다시피 레이블이 되어있는 데이터는 꽤 적네요.

만약 저 decision boundary 즉 빨간선이 없다고 생각해보세요.

사람이라면 왠지 저 빨간색선으로 나눌 것 같은데? 라는 직관에서 이러한 semi supervised learning이 출발합니다.

잘 알려진 semi supervised는 세 가지 모델이 있습니다.

1. Active learning
2. Self-learning
3. Co-learning
   

Semi Supervised Learning- Active learning

Active learning은 “아, 나 다른애들은 어떻게든 하겠는데, 얘는 좀 어렵네 이거 알려줘” 라고 머신이 사람에게 물어보는 방식입니다.

그럼 머신은 사람에게 물어볼 데이터를 어떻게 결정하는 걸까요?

그에 대한 연구도 ongoing인데 크게 두 가지를 소개하겠습니다.

• Uncertainty sampling : 하나의 모델을 학습한 다음에 레이블 뿐아니라 confidence가 몇 점인지도 낸다고 가정을 하는거에요.
  젤 작은 confident를 갖는 데이터의 레이블을 물어보게 되는거죠.
  가장 애매한걸 머신이 사람에게 query하는 것이지요.
  

• Committee-based sampling : 만약 네 개의 모델을 만들었다고하면 각 unlabeled data에 대해 “야 이거 뭐같애?”하면서 물었는데 2:2가 나오면 그때만 사람에게 query 하는거에요.
  3:1이나오면 자기들끼리결정해버리는 거구요.
  
  

Semi Supervised Learning- Self training

레이블이 되어있는 학습데이터(gold dataset)이라고 합시다.

얘를 supervised 학습으로서 생성한 모델 M을 사용하여 unlabeled instance {x1,x2,x3,…}에 대해 예측한 결과 {y1, y2, y3,…}를 얻을 수 있습니다.

Confidence가 높은 일부(silver dataset)을 학습용으로 사용하여 모델 M’을 얻습니다.

위 과정을 우리가 정한 일정조건을 만족할 때까지 반복합니다.

모델이 낸 결과지만 너무나 confidence가 높아서 이건 학습용으로 써도 괜찮을 것 같아 라는 취지에서 나오는 것이 바로 silver dataset입니다.

하지만 자칫 잘못하면 모델이 엉뚱한 방향으로 학습될 수 있다는 단점이 있습니다.

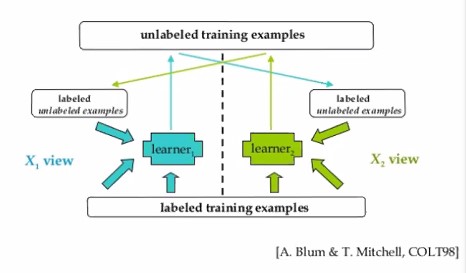
Semi Supervise Learning- Co-learning

Co-learning은 독립적인 모델들이 각각 self-learning을 하되, 서로 간에 confidence가 높은 데이터를 물물교환하는 것을 말합니다.

“이거 내가 보니까 확실하더라! 이거 너도 써” 하고 서로 교환하는거지요.

Q 최종 모델은 그럼 누구로 결정하게될까요?

최종모델을 결정하기 위한 연구들이 이미 존재할꺼야. 사람이 생각할 수 있는 거의 모든 방법은 이미 다 연구되어있다고 봐야 해요. (예: 두 모델을 모두 사용(voting)하거나, 두 모델의 성능 등을 바탕으로 weighted voting 등..)

클러스터링은 레이블이 없어도 쓸 수 있는 모델입니다.
하지만 결국 아주 적다하더라도 레이블은 달려있어야 해요.
클러스터링을 할 때 우리가 원하는 목적의 레이블이 존재해야만 합니다.

예를 들어 우리의 목적은 하마와 기린을 분류하는 것일 때가 있을 것이고 같은 데이터가 있다하더라도 수컷과 암컷을 분류해야하는 것일 수 도 있었다는것이죠.

물론 레이블을 쓰지 않고 measure하는 방법도 있긴하지만 결국 그런 메소드들은 정답 없이 성능을 측정했으니, 결국 진짜 성능이라고 보기 어렵겠지요.

k-means

k-means 알고리즘은 이름에서도 알 수 있듯이 k개의 mean입니다.
mean이 뜻하는 것은 평균값이죠.
그 중심을 기준으로 군집화를 하게 됩니다.

아래 그림을 몇 개의 군집으로 나눠야 잘 나눴다고 할 수 있을까요?

사람들마다 서로 다른 대답을 할 것입니다.
이것이 바로 unsupervised learning의 맹점이죠.

Kmeans 알고리즘의 pseudo code는 아래와 같습니다.

임의의 k값을 정하고 군집별 초기 중심위치를 선택해야 합니다.

데이터i와 1번군집중심의거리, 데이터i와 2번군집중심의거리, … 데이터i와 k번군집중심의거리를 계산해서 가장 가까운 군집쪽으로 할당해줍니다.

거리를 계산할 때 많이 사용하는 것은 유클리드 거리공식(Euclideandistance)입니다.

데이터별로 군집 할당을 끝냈으면, 각 군집별 중심을 다시 계산합니다.

데이터가 할당된 군집이 변경되는 경우가 없어질 때까지 반복합니다.
다른 말로는 중심이 바뀌지 않을 때까지 반복합니다!

그런데 kmeans에 의한 군집화가 엉망으로 되는 경우도 있을 수 있습니다.

왜일까요?

바로 초기값이 어떻게 정해지느냐에 따라서 결과가 좌지우지될 수 있다는 것이죠.
그래서 한 번만 돌려보면 안됩니다.

초기값을 어떻게 줄지에 대한 연구도 많고 관점에 따라 달라질 수 있는 ‘최적’의 cluster 개수를 정하는 것에 대한 연구도 많습니다.

Hierarchical clustering 결과를 활용하여 최적의개수를 짐작하는 방법이 있고 rule of thumb나 elbowmethod, Information Criterion Approch 등의 방법도 있습니다.

Elbow method의 경우 여러 후보 k값들에 대하여, cluster 들의 적절함을 평가하는 것입니다.

적절함 이란 예를 들어 cluster 중심으로부터의 거리 등을 말합니다.

결국 elbow method는 여러 후보값들에 대하여 일일이 시행해보고 관찰하는 면에서 일종의 Grid Search 입니다.

팔꿈치라는 이름이 붙은 이유는 k값을 바꿔가면서 데이터 X의 SSE 값을 그래프로 그려주는 함수로 급격하게 기울기가 변하는 곳이 있는데 그 지점이 최적의 k값이며, 전체적인 그래프를 보았을 때 뾰족한게 팔꿈치같다고ㅎㅎ가 이유입니다.

Information Criterion Approch는 클러스터링모델에 대해 likelihood를 계산하여 활용하는 방법입니다.

예를 들어 K-means의 경우에는 Gaussian Mixture Model을 활용하여 likelihood를계산합니다.

K means는 아까 말했듯이 cluster중심 초기위치에 의해 엉터리 결과가 나올 수 있습니다.
구형(normal 분포)이 아닌 클러스터를 찾을때는 부적절한 결과가 나올 수 있는 것이죠.
Cluster 초기값을 어떻게 결정할 지에 대한 연구들도 많이 있습니다.

k-means는 Outlier에 취약합니다.

해결법은 outlier 제거를 위한 전처리를 해주는 것이며, 또 다른 해결법으로는 k-medoids 알고리즘이 있습니다.
이 방법은 mean을 계산하지 않고, 데이터 중에서 하나를 중심으로 사용하는 방법입니다.

Q 표본데이터중에 하나를 중심으로 뽑는데 그게 만약 튄 값일수도 있지 않을까요? outlier를 제거하는 효과가 있다고 말할 수 있을까요???

K-NN

k-nn(nearest neighbor)알고리즘은 군집화를 위한 모델은 아닙니다.
이전에 kaggle의 유명한 데이터인 titanic dataset과 관련하여 k-nn을 설명한 링크를 참고하시라고 여기에 걸어두겠습니다.

k-NN 알고리즘은 Instance-basedlearning에 속합니다.

Instance-Based Learning의 또다른 말로는 Memory-basedLearning라고도 부릅니다.

Instance-Based Learning이란 학습 데이터로부터 임의의 모델 파라메터를 학습하는 것이 아닌 학습 데이터와 테스트 데이터를 직접 비교하는 것을 말합니다.
그래서 Nonparametric method의 일종이지요.

학습 데이터의 label을 사용하므로 supervised learning에 해당합니다.

k-NN알고리즘은 “내가본 것중에 그거랑 제일 비슷하네!”를 취지로 하는 모델입니다.

이 때 k란 몇 번째로 가까운 데이터까지 살펴볼 지를 의미합니다.

Distance function

심화 질문입니다.
k-means, k-nn알고리즘을 사용할 때 feature normalization을 해야 할까요?

두 알고리즘에서 고려해줄 사항은 k 값, kmeans의 경우라하면 초기 중심값 등이 있을거고 하나 더 고려해줘야 한다면 그것이 바로 feature engineering입니다.

결론적으로는 ‘해야 한다’입니다.

Feature normalization이 잘 되어있어야 distance function의 결과가 합리적으로 나올 것입니다. 그리고 Distance function은 결국 사람이 잘 결정을 해줘야 하는 문제입니다.

Distance function으로는 Euclidean distance가 가장 많이 사용되긴 하지만, Mahalanobis distance 공식도 있습니다.

두 벡터(데이터)사이의 거리를 구하고 싶다 하면 각 차원의 거리별로 차이값을 구한 뒤 제곱해줘서 다 더해주는 것이 Euclidean distance공식입니다.

Distance function은 거리개념이니까 얼마나 머냐 하는 것에 대해서 보는 것이고, Similarity function은 얼마나 비슷하냐를 특정화하는 함수입니다.

우리가 ‘거리’라고 하는 개념은 결국 얼마나 다른 데이터인가를 보는 척도가 되는 것입니다.
차이라는 것은 거리라는 개념으로서 이해하며 distance function을 통해 보는 거고, 얼마나 비슷하니를 보는 것으로 Similarity function가 측정하는 도구가 되는 거지요.

결국 둘 다 distance를 측정할 때 보게 되겠죠.

어지간하면 Euclidean distance 쓰면 되는데 다른 것들도 알아둬서 나쁘진 않지요!

가운데 껴있는 애가 covariance의 역함수이므로 일종의 분모개념으로 이해하시면 편합니다.
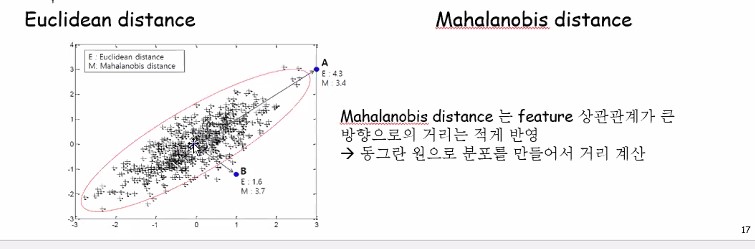
십자표가 다 데이터라고 해봅시다.

Euclidean으로 했을 때는 A까지가 4.3, B까지의 거리는 1.6으로 명백하게 A보다 B가 훨씬 가깝습니다.

근데 Mahalanobis로 보면 오히려 B까지의 거리가 A까지의 거리보다 길어져요. Covariance matrix의 역함수 때문에 데이터 분포의 feature들간의 상관관계가 큰 방향으로의 거리는 적게 반영이 되는 것이죠. 별로 안 먼 것처럼 받아들이게 됩니다.

기하학적인 관점으로 이해하려면 동그란원으로 짜부러뜨려서 동그랗게 만들었다고 생각해봅시다. 그럼 A는 원의 경계선으로부터 아주 조금밖에 벗어나있지 않고 B는 비교적 멀리 벗어나있게 되니까요!

이처럼 동그란원으로 찌그려뜨려 봤을 때 어디가 더 먼가를 보는 것이 바로 Mahalanobis distance입니다.

similarity도 distance를 잴 수 있다고 했었는데 코사인 similarity도 쓸 수 있습니다.

여러 가지가 있으니까 knn, kmeans에 뭘 쓸까 고민되실 때는 찾아보시면 되겠습니다.

Hierarchical clustering

K-means 다음에 hierarchical clustering을 보는 게 순서가 더 맞을 수 있을지도 모르지만 K-nn이 사이에 낀 이유는 그저 이름이 비슷해서요 ㅎㅎ.

계층적 클러스터링, Hierarchical clustering을 배웁니다.
Hierarchical clustering의 알고리즘은 아래와 같습니다.

1. 각 데이터들을 cluster라고 가정합니다. 임의의 cluster 개수를 정해놓지 않는다는 것에 집중해주세요. 최적의 클러스터 개수를 가정하고 있지 않아요. 모든 데이터를 클러스터라고 가정하는 것이지요.
   
2. 각데이터 pair 사이의 distance를 계산합니다. Distance 개념이 또 나왔죠. 당연한 이야기지만 distance function을 뭘 쓰느냐에 따라서 결과가 달라질 것입니다.
   
3. 가장 distance가 작은 pair를 하나의 cluster로 묶습니다. 데이터 두 개 두 개 씩 짝지어서 모든 pair를 다 봐야 하니까 n개의 데이터가 있으면 nC2만큼 거리를 계산해줘야겠죠?
   

어쨌든 지금까지의 distance를 다 계산해놨다 하고 모든 pair중에서 distance가 가장 작은 것!
즉, 가장 비슷한 짝꿍들을 하나의 클러스터로 묶어주는 작업을 하게 됩니다.
그렇게 모든 데이터가 하나의 클러스터로 묶일 때까지 2-3번을 반복합니다.

저런식으로 서서히 묶이게 될 것입니다.

차례대로 클러스터링 과정을 보이는 그림입니다.
ab가 묶였으니까 이건 새로운 클러스터로 취급해주고 다시 계산해줘야 해요. 가장 가까운 거리끼리 또 묶어줘요.
이렇게 반복하고 있다 보면 모든 데이터가 한 개의 클러스터로 바뀐 것을 볼 수 있습니다.

이 그림이 지금은 눕혀져 있지만 세워놨다고 생각해보세요.
마치 트리 같지 않나요? 제일 끝에 나온 결과가 루트 모양이고 왼쪽이 단말노드라고 생각해보면 그야말로 hierarchical 합니다.

당연한 이야기지만 오른쪽으로 가면 갈수록 응집화된 클러스터겠죠.
우리가 군집 개수를 알려주진 않았지만 잘 군집화를 해주네요.

예전에 배웠던 것을 떠올려봅시다.
군집이 잘 된 건지, 군집개수는 적절한지를 알아볼 때 사용되는 것이 바로 hierarchical clustering입니다.

군집개수를 다섯 개로 한다고 하면 젤 왼쪽꺼고, 군집개수를 두 개로 한다 하면 ab, cde 이렇게 할 수 도 있을거고, 군집개수를 세 개로 한다 하면 ab, c, de 로 할 수 도 있는 것이구요.

따라서 hierarchical clustering은 아주 단순하지만 효용가치가 높은 알고리즘 이라고 할 수 있습니다.

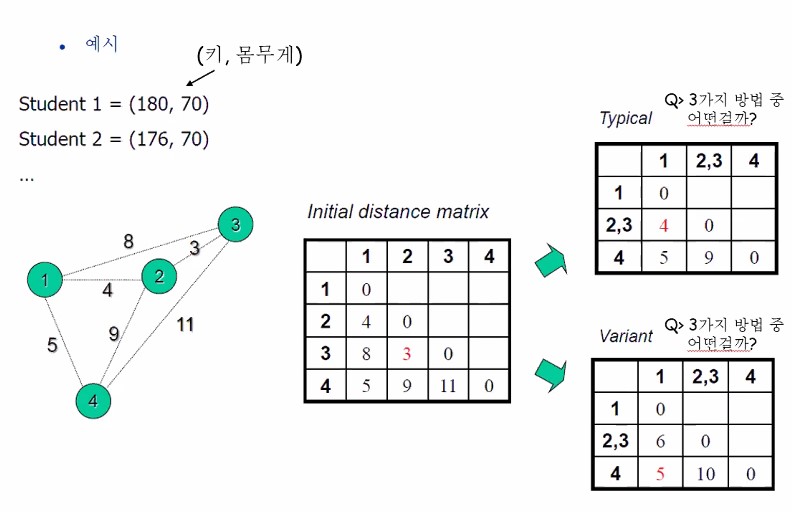
예시를 구체적으로 한 번 더 봅시다. 왼쪽 그림과 같이 데이터가 2차원 공간상에 총 6개 존재한다고 합시다.
알고리즘 대로라면 Pair들 사이의 distance를 계산해주지요.

디스턴스 매트릭스를 구해서 갱신해가는 과정을 보여주고 있습니다.
방향성은 보지 않고 있으므로 대각성분의 왼쪽아래 성분들만 채워놓았네요.
저 제일 아래 그림이 덴드로그램입니다. 덴드로그램으로 표현할 줄 알아야해요.

두 cluster간에 distance를 잴 때, 어떤 방식으로 distance를 재느냐에 따라 여러가지 변형이(variatns)가 존재합니다.
이제 Distance function을 고르는 것이 중요한 것이 아닙니다.
distance를 잴 때 policy(정책)이 무엇인가도 정해줄 필요가 있습니다. policy라는 것은 군집과 군집사이의 디스턴스를 재는 방식에 대한 것을 말합니다.

Step4에서 123,45,6 세 개 군집 사이의 거리를 잴 때 4와 6간에 거리를 할건지, 5와 6사이의 거리를 할건지 애매한거죠. 어느 놈이 우리의 대표냐를 못 정했어요 아직!
이 문제는 어느 공식을 쓸 것인가에 대한 고민을 하는 단계가 아니에요.
‘유클리드’라는 줄자를 쓸지, ‘마할라노비스’라는 줄자를 쓸지는 이미 정해져 있다고 하고,

policy라는 것은 줄자를 뭐로 쓸지 얘기가 아니라 어떻게 두 군집 사이를 정의하겠냐라는 문제인 것입니다.

민트색 군집의 데이터와 빨간색 군집의 데이터의 거리를 잴 때, element 사이의 거리를 직접 재는거에요. 그룹에서 잴 때, 민트색 그룹에 13 두개있고, 빨간 그룹에 426있는데, 그 중 가장 안쪽에 있는 한 놈씩 대표로 선출해서 잴 건지, 아님 다 재고 평균 낼 건지를 고민하게 됩니다.

전자가 싱글링크, 후자가 에브리지링크, 젤 먼놈둘이 (3,6)거리재는게 컴플리트 링크입니다.

위쪽은 싱글링크, 아래쪽은 에브리지 링크요

Distance matric을 어떻게, 어떤 link를 사용하는지에 따라 다른 결과가 나온다는 것을 기억합시다.

average link를 사용했을 때 성능이 가장 좋았다는 연구 결과가 있습니다.

이러한 특징을 갖는 Hierarchical clustering은 덴드로그램을 통한 시각정보를 제공한다는 것과 시각화나 사용에 용이하다는 이유로 널리 사용됩니다.
하지만 O(n^2)의 시간 복잡도를 갖고 이전 스텝에서의 실수를 수정할 수 없다는 단점을 갖습니다.

Variant

흰색 냉장고와 흰색 지우개를 색으로만 distance 구할 경우 distance는 거의 0입니다. 그러나 크기로 distance 구할 경우 distance는 어마어마할 것입니다.
그래서 feature engineering이 매우 중요합니다.

다른 이야기) 딥러닝의 대가들 중 튜링어워드를 받았던 요슈아 벤조라는 사람이 어텐션이라는 기술을 소개했습니다. 그 기술이 컴퓨터로 하여금 인공지능으로 하여금 자아를 가지게 할 핵심기술이 될 것이다 라고 발표했다고 합니다.

Similarity의 반대는 dissimilarity 또는 distance이라고 할 수 있습니다.
아마도 아래 예제에서 여러분은 x1,x2를 하나로 묶고 x3,x4를 하나로 묶었을 겁니다.

머리카락길이는 category 데이터로 두었네요
여러분들이 어떻게 저렇게 나눈 걸까요? 여러분들이 순간적으로 거리를 재본 겁니다.

Similarity와 distance는 동전의 양면과 같습니다.

기본적으로 위 두 가지, Euclidean distance와 cosine similarity를 많이 씁니다. 필요할 때 찾아서 사용해보시길 권장드립니다.

카테고리컬은 다르면 1 같으면 0로 distance를 두었네요. 키랑 몸무게는 좀 다른 문제지요. 값의 range가 다르잖아요?

Feature engineering이 안되어있기 때문에 저 categorical feature는 1또는 0이니까 상대적으로 묻히는 거지요. 그래서 normalization을 해줘야합니다.

유클리드 디스턴스의 특징

1. x부터 y까지의 거리는 0보다 크거나 같고, 자기자신과의 거리는 0
   
2. 순서와 상관없이 x에서 y까지의거리는 y에서 x까지의 거리와 같고
   
3. x에서 k를 경유해 y를 간다면 x에서 k까지의 거리와 k에서 y까지의거리의 합보다 x에서 y까지의 거리는 크거나 같다. 이러한 특징은 triangle inequality입니다.
   

Short hair 처럼 categorical feature나 누락된 데이터는 어떻게 해주는 게 좋을까요?

누락된 데이터(missing value)를 다루는 방법은 크게 두 가지를 소개해드리겠습니다.

크게 두 가지 방법이 있습니다.

첫 번째 방법은 버리기 입니다. 가로축을 버릴 수도 있겠지만, 세로축을 버릴 수도 있습니다.

두 번째 방법은 데이터를 버리는게 아니라 다 안고 가는 거에요.
그러려면 채워줘야 하잖아요?
구멍을 완벽하게 메꿔준다라고 해서 matrix completion이라고 부릅니다.
전체 그 열 값들의 mean값으로 채우는 거에요. 전체 평균치로 넣는거지요. 제일 단순하고 제일 무책임한 방법입니다.

또 0으로 주는 방법이 있습니다. 그런데 이렇게 0으로 줘버리게 되면 대부분의 경우에는 성능에 악영향을 끼쳐요.

왜냐하면 몸무게가 진짜 0인 사람이 있을까? 이런 것까지 생각해줘야한다는 것이죠. 만약 또 다른 케이스로 0인 값이 들어올 수 있다고 하면요, 진짜 0인 경우와 결측치여서 임의로 메꿔준 경우가 구분이 되지 않을 것입니다.

그런 문제가 발생하지 않는 또 다른 케이스라해도 Feature normalization할건데 어차피 0~1사이로 하지 않겠나요? 그런데 missing value를 0으로 둔다면 스케일링 했을 때 가장 작은 값이라고 생각하겠지요.. 그래서 0으로 채우는건 아주 비추천하는 방법입니다.

차라리 mean 값이 낫습니다.

여러분이 현실 세계에서 만나는 데이터의 대부분은 안타깝게도 지저분하며 결측치가 어마어마하게 많습니다. Outlier도 엄청 많아요.

전체 데이터의 90퍼센트 이상이 결측치라면 아예 drop해버리는 것이 낫겠죠.

Q 결측치 채울 때 원 데이터를 조작하는 것은 아닐지 고민입니다.
A 데이터 조작 아니에요! 명시만 하면요.
하지만 데이터를 채워 넣기 위한 imputation이란 기법이 있어요.

Imputation 알고리즘도 missing value를 채워넣는 방법입니다.
Imputation 구현 코드 url: https://github.com/epsilon-machine/missingpy

Missing value들은 채워 넣는 것이 항상 적절한 걸까요?
너 그거 채워 넣으면 안되는거잖아 하는 기준이 있습니다.
아래는 언제 채워 넣는 것이 좋고 언제 채우면 안되는 것인지에 대한 용어에요. MAR과 MCAR 둘다 imputation해도 되는데 MNAR일 때는 하면 안됩니다.

• MAR(Missing at Random) : 특정 변수(feature, variable)의 결측치들이 무작위로 발생
  
• MCAR(Missing Completely at Random) : 완전히 무작위로 결측치 발생
  
• MNAR(Missing Not at Random):결측여부가 해당변수의 값에 의해 결정
  

예를 들어서 아래와 같이 선수에 대한 데이터가 있습니다.
입단을 원해서 이력서를 냈다고 합시다. ㅎㅎ

자기 나이에 대해서 30대 이상이면 안 뽑을 거라는 걱정이 되어서 나이를 안 썼다고 합시다.
이런 경우에는 우리가 결측치를 다른 값으로 채워 넣는 게 바람직할까요?
데이터를 획득하는 과정에서 의도치 않게 결측치가 발생했다면 채워 넣어도 괜찮지만 어떤 특정 의도하에 결측치가 지속적으로 발생했다면 그건 채워넣으면 안되는 것입니다.

정리하자면 랜덤하게 결측치가 발생한 것이 아니라면 결측치를 함부로 채워넣으면 안됩니다. 그때는 데이터 조작이다 라고 욕을 먹게 됩니다. 나중에 더 자세히 다뤄보겠습니다.

심화 질문 입니다.
(1.0, 582, black)과 같이 여러 타입의 feature가 석여있는 경우에는 유사도 계산을 어케하는가?

Real number랑 catergorical data가 함께 있을 때요! 아까 얘기했지만, categorical은 보통 같으면 0 다르면 1로 값을 주지만, 각 feature 값들의 range가 다르니 normalize를 해줄 필요가 있다라구요.

심화 질문 두 번째입니다.
외계종족이 몸무게가 50~100kg이며, 키가 2~2.5cm 라면? 이 경우의 문제는 단위가 다르다는 점이며, 이에 대한 해결법으로는 normalize을 해줘야 합니다.
Distance를 잴 때 normalization안하고 학습시키면 엉뚱한 결과가 나오게 될 것입니다.

거리를 재는 여러 방법들 중 또 하나를 더 소개하자면, KL divergence가 있습니다. KL divergence로Mutual Information을 표현할 수 있습니다.

Mutual Information이란 두 변수 x와 y가 얼마나 독립적인지를 판단하는 방법으로 두 변수간의 convariance가 없는가 에 대한 값입니다. x와 y가 서로 독립이라면 P(x,y) = p(x)p(y)가 성립합니다. 이러한 두 확률변수간의 독립을 p(x,y)와 p(x)p(y)간 KL-divergence로 표현하면 아래와 같습니다.

출처 : https://jgshin.tistory.com/12

두 변수가 독립이라면 KL-divergence 식의 값은 0이 나옵니다.
그리고 이 때 I[x,y]를 확률변수 x,y간의 mutual information이라고 부릅니다.
X만 관찰했을 때의 확률 분포랑 y를 반영한 x의 확률분포간의 차이를 표현한 식인 것이지요.

개인이 공부하고 포스팅하는 블로그입니다. 작성한 글 중 오류나 틀린 부분이 있을 경우 과감한 지적 환영합니다!

(추가 내용) Feature 값의 scaling 방법은 normalization과 standardization이 있습니다.

L1,L2 regularization위해서는 feature normalization을 해줘야합니다. Standardization은 Normal 분포의 standard derivation 값을 가지고 변환시키는 방법을 말합니다.

Missing feature value가 있는경우 그들을 다루는 일반적인 방법은 아래와 같습니다. Distance 값이 0~1사이라고 가정할 때 Categorical (nominal) feature 두 데이터 중 한쪽이라도 missing이면 1을 주고 Numerical feature의 경우에는 ㅇㅇㅇ

Imputation algorithm의 한 종류인 KNN은 k값이 성ㄴ능을 좌우하는 알고리즘이져

Entropy 기억나시죠? Discrete case가 있고 Continuous case가 있습니다.

KL(Kullback-Leibler) Divergence를 Relative entropy라고도 부릅니다. KL divergence는 두개의 distribution 간의 차이를 measure하는 것으로 같으면 0 다를수록 커집니다. 차이라는 말이 애매하지만 거리개념은 아니랍니다.

크로스엔트로피에서 자기자신 엔트로피를 뺀다는 것은 얼마나 잘섞여있고 정리되어있는가를 측정할 도구가 되는 것입니다. 엔트로피가 정보량이 많다 적다를 나타내는 값이었죠? 식이 저렇게 되다보니까 뭐에서 뭘빼냐는 것에 따라 달라집니다.

그렇기 때문에 거리의 개념으로 보기엔 애매합니다. 그래서 relative entropy라고 부르는 겁니다 Mutual information은 두 개의 random variable 들이 얼마나 의존적인지를 measure합니다.

얼마나 차이가 나니를 보는 거거였잖아요? 앞에껀 joint probability고 뒤에는 따로따로 존재하는 텀이잖아요? 그럼 결국 의미하는 것은 ‘독립’성에 비해 얼마나 ‘의존’성이 강한지를 측정하고자하는 것이지요.

우리는 kl divergence가 뭐엿는지를 잘 기억해야합니다.

잘 떠올려보세요 EM LDA 이런알고리즘들 사이에서 우린 봤어요 Z라는 variable은 값이 계속 변할 수 있잖아 그건 말 그대로 변수거든여 그런 식으로 샘플링해서 생기는 값을 random variable이라고하는 것입니다.

우리가 Hierarchical Clustering를 정리해봅시다 이 모델의 장점은 시각적 관점으로 해석하기에 아주 용이한 덴드로그램으로 표현해낼 수 있다는 것입니다. 또한 쉽습니다. 단점은 O(n^2)의 부담스러운 시간복잡도를 갖는다는 점입니다. 또한 계층적이라는 구조 특성상 앞선 단계에서 오판단을 할 경우 수정할 수 없다는 것입니다.

우리 배웠던 군집별 정책 중 Averagelink 방식이 가장 성능이 좋았다는 연구결과가 있다합니다. 거의 대부분의 군집화 알고리즘들이 겪는 문제로 군집 개수를 결정하는 문제가 있습니다.